Статья посвящена фундаментальным понятиям теории вероятности, необходимым инвестору для операций с ценными бумагами. В доступной форме дана трактовка вероятности, математического ожидания, среднеквадратичного отклонения и ряда других терминов и явлений в контексте фондового рынка.
СОДЕРЖАНИЕ:
1. Введение. Из истории вопроса и важные определения
2. Вероятность
3. Сложение и умножение в теории вероятностей
3.1. Сумма событий и сложение вероятностей
3.2. Произведение событий и вероятностей
4. Математическое ожидание
5. Дисперсия
6. Среднеквадратичное (стандартное) отклонение
7. Функция плотности вероятности
8. Нормальное распределение
Примечания и ссылки
Используемые сокращения
Первыми попытками понять, систематизировать и, в определенной степени, предвидеть поведение случайных величин, человечество обязано банальной теме азартных игр. «Орел или решка», игральные кости и рулетка заставили задуматься над сутью проблемы вначале рискованных игроков, а потом и серьезных ученых-математиков.
В XVII веке два выдающихся французских мыслителя Блез Паскаль и Пьер Ферма исследуют закономерности, возникающие при бросании игральных костей. Примерно в это же время предметом вероятностей начинает интересоваться голландец Христиан Гюйгенс. Публикация профильной работы Х. Гюйгенса пришлась на 1657 год. В ней вводятся такие ключевые моменты, как вероятность события, математическое ожидание, правила сложения и умножения вероятностей. Переписка Паскаля и Ферма увидела свет чуть позже, в 1679 г.[1].
Свою современную форму теория вероятностей приобрела относительно недавно, менее 100 лет назад, благодаря вкладу советского математика Андрея Колмогорова. Он формализовал теорию вероятностей, дав ей математическое описание. Благодаря предложенной А. Колмогоровым аксиоматике, теория вероятностей стала частью классической математической науки[2].
1. ВВЕДЕНИЕ. ИЗ ИСТОРИИ ВОПРОСА И ВАЖНЫЕ ОПРЕДЕЛЕНИЯ

А.Н. Колмогоров (1903-1987)[3]
Википедия [1] определяет теорию вероятностей, как «раздел математики, изучающий случайные события и случайные величины, их свойства и операции над ними».
Выделенные курсивом сочетания не просто слова, как покажется на первый взгляд, они имеют строгие математические определения.
Случайное событие – один из исходов (часть множества) случайного эксперимента[4], математической модели реального эксперимента[5].
(далее по тексту при описании случайного события, для краткости, может применяться просто слово «событие»)
Случайная величина – значения переменной, представляющие исходы случайного события. Другими словами – «численное выражение результата случайного события»[6].
Итак, случайное событие – некий исход эксперимента, случайная величина его численное значение. Например, после броска кость (кубик) опустится на одну из шести граней – имеем случайное событие. Число очков каждой грани, от одного до шести – случайная величина, численное выражение случайного события.
Прикладное значение теория вероятностей получила не сама по себе, а вместе с математической статистикой. Под матстатистикой понимают « раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов, с целью построения вероятностных моделей массовых случайных явлений»[7].
Прежде всего, рассмотрим базовые понятия теории вероятностей (ТВ), без которых углубляться в тему нет смысла.
(далее, по тексту, кроме приведенных в конце статьи источников, автор опирается на книгу Е.С. Вентцеля «Теория вероятностей», издание 1999 г.)
Прежде всего, что такое вероятность.
Вероятность – «степень (относительная мера, количественная оценка) возможности наступления некоторого события»[8].
Общеизвестная формула расчета вероятности дискретного (не непрерывного) события А в системе равновозможных и исключающих друг друга исходов опыта имеет вид:
P(A) = n/N (формула 1)
где:
P(A) – вероятность события А;
n – число случайных (несовместных равновероятных элементарных) событий, приводящих к событию А
N – общее количество всех возможных элементарных событий.
Наглядным примером вновь может послужить все та же игральная кость. Пусть событие А – выпадение нечетного числа очков: А=нечет. Оно формируется тремя элементарными случайными событиями, имеющими величины: 1, 3 и 5. То есть n=3. Общее количество всех элементарных событий N = 6. Имеем P(нечет) = 3/6 = 1/2.
Вероятность определяется дробью от 0 до 1 или в процентах, от 0% до 100%.
Для случая неограниченного числа N или, если необходимо максимально нивелировать такие исходы, как, допустим, застывание монетки на ребре (ни орел, ни решка) после ее подбрасывания, формула 1 обобщается следующим образом:
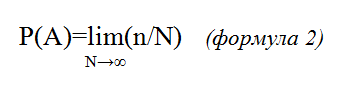
То есть, предел (lim) отношения n/N при N → ∞
Здесь N – число проводимых наблюдений (экспериментов), смысл n тот же, что и в формуле 1.
Если подходить совсем общо, и рассматривать не дискретные, а непрерывные случайные величины, то вероятность можно понять и вычислить, применяя геометрию.
Предположим, нас интересует вероятность попадания точки в треугольный сегмент g, площадью s(g). В свою очередь, треугольник g входит в овал G, площадью S(G), при этом за пределы G точка выйти не может.
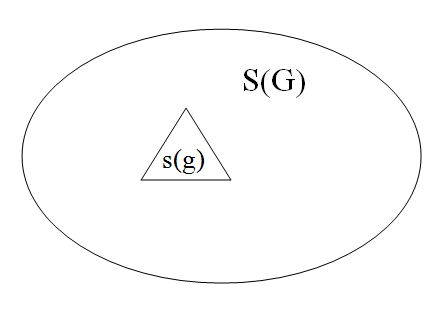
Имеем:
P(A) = s(g)/S(G) (формула 3)
где P(A) – вероятность попадания точки в треугольник g, площадью s(g).
3. СЛОЖЕНИЕ И УМНОЖЕНИЕ В ТЕОРИИ ВЕРОЯТНОСТЕЙ
События в ТВ можно складывать и умножать.
3.1. Сумма событий и сложение вероятностей
Суммой двух случайных событий X и Y называется событие Z = X + Y, заключающееся в наступлении события X или события Y, или обоих событий одновременно.
Вероятность суммы двух несовместных событий (событий, которые не могут произойти совместно, одновременно) равна сумме их вероятностей (теорема сложения вероятностей):
P(X+Y) = P(X)+P(Y) (формула сложения вероятностей)
Если события X1, X2, …. Xn образуют полную группу несовместных событий, т.е. при любом исходе случится какое-либо одно из этих событий, то сумма их вероятностей равна 1:
P(X1+X2+….+XN) = P(X1)+P(X2)+….+P(XN) = 1
Простейший пример – подбрасывание монеты. Имеем два несовместных, в данном случае, говорят «противоположных» события, вероятность каждого по ½. Событие X – выпадение орла, событие Y – решка. Событие X+Y состоит в наступлении либо X, либо Y. Это произойдет в любом случае (кроме того, когда монета станет на ребро). Вероятность P(X+Y) = P(X)+P(Y) = 1\2+1\2 = 1.
Примером из фондового рынка может стать цена акции А, разбитая, допустим на три диапазона:
1) установление цены до $80 – событие X;
2) от $80 и до $100 – событие Y;
3) свыше $100 – событие Z;
Очевидно, что события X, Y и Z образуют полную группу несовместных событий. Пусть вероятности наступления событий X, Y, Z соответственно равны P(X) = 0,5; P(Y) = 0,2; P(X) = 0,3.
Тогда возможны такие комбинации сумм событий:
X+Y – цена в интервале от 0 до $100, вероятность 0,5+0,2=0,7;
Y+Z – цена свыше $80, вероятность 0,2+0,3=0,5 (наименее вероятное событие, равное сумме двух событий);
X+Z – цена в интервалах до $80 и свыше $100, вероятность 0,5+0,3=0,8 (наиболее вероятное событие, равное сумме двух событий);
X+Y+Z – стоимость лежит во всем ценовом интервале (0;+∞), естественно, вероятность по полной группе событий равна 0,5+0,2+0,3=1
3.2. Произведение событий и вероятностей
Произведение событий X и Y – событие Z = X*Y, состоящее в одновременном (совместном) появлении событий X и Y.
Вероятность произведения двух независимых событий равна произведению их вероятностей (теорема произведения вероятностей):
P(X*Y) = P(X)*P(Y) (формула умножения вероятностей)
События считаются независимыми, если вероятность наступления одного из них не зависит от наступления другого. С другой стороны, события зависимы, если вероятность одного из них зависит от того, случается ли другое событие.
Примеров зависимых событий на финансовых рынках миллионы, они ими пронизаны. Искусство опытного трейдера – разглядеть влияние отдельного факта на тренд конкретной бумаги. Вероятность и степень движения в ту или иную сторону. Инсайдерская информация доступна далеко не всем, впрочем, ее использование преследуется (и весьма жестко) контролирующими органами. Часто вполне достаточно открытых сведений.
Из недавнего можно привести инцидент с катастрофой авиалайнера Боинг-737 Эфиопских авиалиний, происшедшей неподалеку от города Бишофту (Дэбрэ-Зэйт), в воскресное утро10 марта 2019 г. Погибли все: 149 пассажиров и 7 членов экипажа.
Трудно сказать, насколько именно падение конкретного эфиопского самолета могло повысить вероятность обрушения акций американской корпорации The Boeing Company. Но эфиопская трагедия стала № 2 в черном списке модели Boeing 737 Max. В конце октября прошлого года аналогичный Боинг упал в Яванское море после вылета из аэропорта Джакарты. Интервал между катастрофами менее пяти месяцев.
Boeing 737 Max – совсем свежая модификация пассажирского Боинга, эксплуатируется с 2016-17 гг. По информации компании ProFinance, к началу текущего года мировые авиакомпании закупили 350 лайнеров. Если за неполные пять месяцев разбиваются две новые машины, значит, есть критичные конструктивные дефекты. Это прямой удар по имиджу авиастроителей. Многие перевозчики могут заблокировать полеты Boeing 737 Max (что действительно и произошло).
Все это грозит немедленно отразиться на котировках акций The Boeing Company. Отразиться негативно.
С точки зрения механики зависимых событий в теории вероятностей, событие X – падение эфиопского Боинга и событие Y – поведение тренда акций корпорации «Боинг» очень и очень зависимые события. Наступление события X в воскресенье 10-го привело к резкому изменению (росту) вероятности крутого пике акций The Boeing Company (тикер BA) на бирже в понедельник утром.
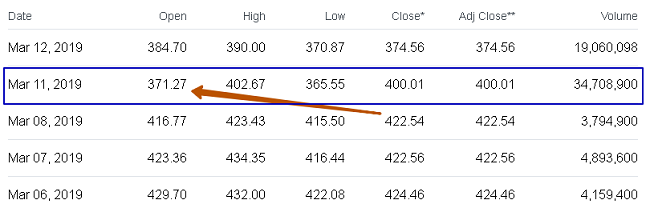
Торги на NYSE (Нью-Йоркской фондовой бирже) открылись 11 марта просадкой на 12 с лишним процентов относительно закрытия дня пятницы 8 марта:
источник[15]
Минус $51,27.
The Boeing Company входит в корзину S&P500 и промышленного Доу-Джонса (DJIA). Последний из-за Боинга на открытии снижается на 0,7%.
В течение дня отрицательный гэп несколько компенсировался и сессия закрылась, потеряв «только» 5,33% против закрытия 8-го. Во вторник 12.03 падение акций авиагиганта возобновилось.
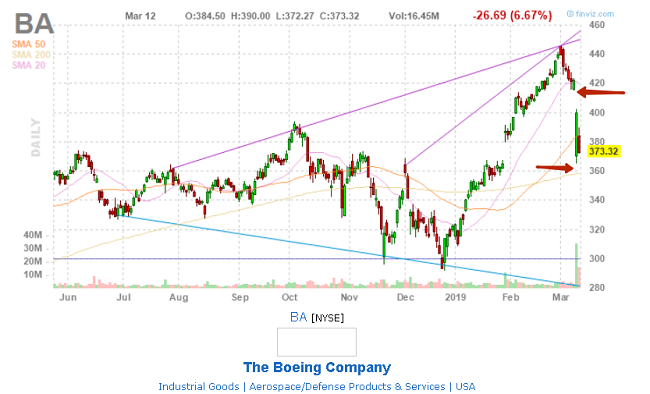
источник[14]
Математическое ожидание случайной величины (матожидание, МО) – среднее значение величины при стремлении числа ее измерений (испытаний/экспериментов) к бесконечности[9]. Функция «Матожидание от «Х» записывается, как М(X).
(Внимание! Здесь и далее по тексту латинскими буквами X, Y, Z и пр. обозначаются случайные величины (их значения), а не случайные события)
Если речь идет об одномерной случайной величине, то оценкой МО может служить ее среднее арифметическое значение[10].
Матожидание обладает следующими простейшими свойствами.
1) МО числа (константы), равно этому числу:
М(С) = С (формула 4)
2) МО имеет линейный характер:
М(aX+bY) = aM(X)+bM(Y) (формула 5)
где a, b – постоянные коэффициенты.
3) Матожидание сохраняет неравенство:
если X < Y, то М(X) < М(Y) (формула 6)
4) МО произведения двух независимых (некореллированных) величин определяется, как произведение их матожиданий:
М(X*Y) = M(X)*M(Y) (формула 7)
Свойства 2 и 4 матожидания прямо корреспондируют с теоремами сложения и умножения вероятностей, изложенными выше.
В трейдинге понятие матожидания (среднего значения) цены инструмента используется в инвестиционной стратегии Mean reversion («Возврат к среднему»). Она предполагает, что на относительно спокойном рынке стоимости акций, валют, деривативов, доходности облигаций группируются вокруг своих средних значений. Любой существенный ценовой выброс за пределы таких средних со временем сменится возвратом к равновесной цене. В свою очередь, матожидания также могут плавно или скачкообразно изменяться во времени.
Если есть матожидание (среднее значение) случайной величины, то логично попытаться понимать, как далеко величина отклоняется от своего среднего. Чем выше разброс или, как иногда говорят, «рассеивание», тем труднее просчитать, проанализировать поведение рассматриваемой переменной и дать толковый прогноз на будущее.
Отклонение случайной величины X от своего среднего M(X) бывают, как в большую, так и в меньшую сторону. Для того, чтобы знак «не путался под ногами», оценкой отклонения вполне мог бы быть модуль разности |X-M(X)|. Но при всей своей простоте, функция «модуль некоего выражения (числа)» не очень удобна для математической обработки.
Математики делают, обычную для них в таких случаях вещь – возводят исследуемую разницу в квадрат.
В теории вероятностей в качестве меры разброса случайной величины X относительно ее математического ожидания прижился параметр, получивший название «дисперсии». Dispersio на латыни – «рассеяние».
Записывается дисперсия, как D(X). В англоязычной литературе получило распространение обозначение Var(X), от англ. variance[11].
Матвыражение дисперсии в общем случае имеет вид:
D(X) = M[(X-M(X))2] (формула 8)
Подобная математическая конструкция столь же красива, сколь и крайне трудна, а часто и бесполезна в практическом применении. В действие вступают различные интерпретации и упрощения формулы 8 для тех или иных случаев.
Например, для дискретной величины X используется следующий вариант:
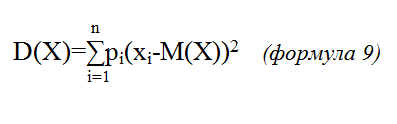
где:
∑ - знак суммы (суммирования) слагаемых с изменяющимся индексом i, пробегающим значения от 1 до n.
pi – вероятность того, что случайная величина X примет значение xi;
n – число измерений случайной величины.
Сказать, что стало намного легче, было бы преувеличением. Где брать/считать вероятности pi ?
Здесь на помощь практикам, в том числе и имеющим отношение к рынку ценных бумаг, приходят две канонические формулы расчета дисперсии[12].
Для отдельной выборки:
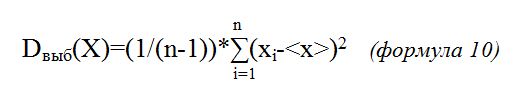
где: <x> – среднее арифметическое случайной величины X:
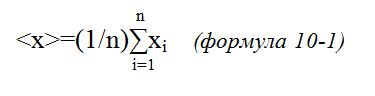
прочие обозначения раскрыты в пояснении к формуле 9.
Для генеральной совокупности:
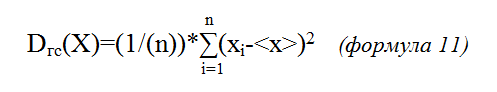
Формула 11 отличается от формулы 10 только знаменателем множителя, стоящего перед знаком суммы ∑: 1/n вместо 1/(n-1). Для генеральной совокупности он на единичку больше. При n → ∞ и, даже, просто при сравнительно большом n (не менее нескольких десятков) обе формулы дают почти одинаковые численные результаты.
Поясним несколько моментов.
1) Использование среднего арифметического вполне понятно. Простейшее приближение матожидания случайной величины, о чем уже было упомянуто выше. То есть, <x> выполняет роль M(X). В этом смысле, <x> ≈ M(X).
2) Генеральная совокупность – совокупность всех значений случайной величины X[13]. Соответственно, отдельная выборка – часть генеральной совокупности.
6. СРЕДНЕКВАДРАТИЧНОЕ (СТАНДАРТНОЕ) ОТКЛОНЕНИЕ
Размерность дисперсии – квадрат отклонения случайной величины от среднего значения. Что нужно делать для оценки абсолютного значения (модуля) такого отклонения?
Извлечь квадратный корень (возвести в степень ½).
Полученный результат именуется одним из центральных в теории вероятностей и матстатистике терминов – среднеквадратичным (среднеквадратическим) или стандартным отклонением, сокращенно СКО. Общепринятое обозначение для СКО – греческая σ.
Итак, все лаконично и красиво:
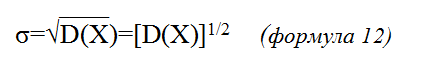
Для отдельной выборки:
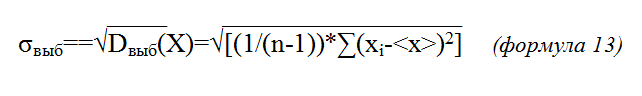
Для генеральной совокупности:
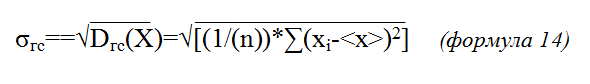
Квадратный корень берется из всего выражения, стоящего внутри квадратных скобок. Индекс i, по-прежнему, пробегает значение от 1 до n.
Как и дисперсия, СКО данной случайной величины зависит от числа ее измерений n. Чем больше n на выбранном временном периоде, тем более четкую картинку по σ мы получим.
Относительно ценной бумаге СКО – мера ее неопределенности, волатильности. Чем выше СКО по портфелю ЦБ, тем он более рискованный в обе стороны. Для трейдера СКО по финансовому инструменту – индикатор его риска. Возможность много потерять, но и много заработать.
СКО вычисляется десятками специальных приложений в техническом анализе. Самый доступный путь – формулы в Excel: «СТАНДОТКЛОН» и «СТАНДОТКЛОНП». Первая дает СКО по выборке (σвыб), вторая – по генеральной совокупности (σгс).
Пример. Акции Facebook (FB)
Расчет и «примитивный» анализ СКО проведем по динамике акций Facebook (FB) в январе-феврале текущего года.
Тренд бумаги выглядит так[14]:
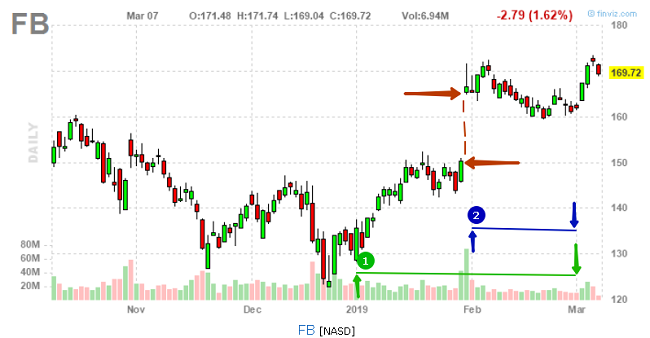
СКО вычислим для двух периодов: 1 января – 28 февраля 2019 г. (цифра 1 зеленые отрезок и стрелки) и только февраль (цифра 2 и синий цвет).
Котировки инструмента из источника[15]. Экспортировав цены закрытия дня (всего 31 значение) и применив функцию для отдельной выборки «СТАНДОТКЛОН», получим σ = $11,63.
Кстати, результат можно проверить. Раздел Excel «Статистические функции» содержит инструменты для вычисления дисперсии. Для выборки – функция «ДИСП», для генеральной совокупности – «ДИСПР». Подставив наше 31 значение в ряд аргументов ДИСП, получим D = 135,35 («долларов в квадрате»). √135,35 = 11,63, с учетом округления, все абсолютно точно.
σ = $11,63 – много это или мало?
Для простейшей оценки, сравним σ со средним (среднеарифметическим, <x>) значением нашей выборки котировок FB. Опять же, обратимся к Excel. Раздел статфункций содержит «СРЗНАЧ», определяющее среднеарифметическое. Для исследуемого массива данных имеем <x> = $154,06. Такова средняя цена акции Facebook на периоде 01.01-28.02.2019. Отношение СКО к средней стоимости акции составляет 11,63/154,06 = 7,55%. Кажется, что немало.
Чтобы утвердиться в своем мнении, посчитаем СКО только для февраля, с 1 по 28 число (19 торговых дней).
Пройдя описанный выше нехитрый алгоритм, имеем:
СКО = $3,06;
среднеарифметическая стоимость, по ценам закрытия - $164,81;
отношение СКО к средней цене – 3,06/164,81 = 1,85%.
Видим, что относительное СКО февраля в 4 раза меньше относительного СКО января-февраля. В последний зимний месяц акции FB вели себя гораздо менее волатильно.
Причина проста и понятна при самом беглом взгляде на график инструмента. В самом конце января (с 30 на 31 число) акции резким гэпом поднялись вверх (красные стрелки на графике).
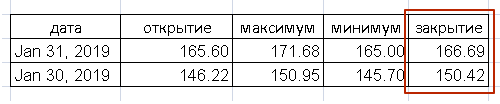
источник[15]
По ценам закрытия, рост составил более $16 или почти 11% (10,82%)! Максимум 31 января превосходит максимум 30 января на $20,73 или на 13,7%. Высокое СКО обусловило высокий риск игрока.
Лонгеры (держатели длинных позиций) за сутки увеличили стоимость своих вложений в FB на 10,82% или на 10,82*365 = 3948% годовых! За это и любят фондовый рынок. Где еще есть такие подъемы?
Те, кто поставил на коррекцию акций, прогнозируя, что они уйдут на поддержку в $125-130 упомянутые 10% потеряли. Вот за это фондовый рынок ненавидят.
В феврале все проходило гораздо более гладко. По СКО – в 4 раза.
Необходимо отметить, что в «боевой обстановке» СКО обычно рассчитывают на текущую дату (момент). Предположим, на 7 марта 2019 года. Тогда при n = 30, берутся 30 торговых дней, предшествующих 07.03.19, то есть, до 06.03.19 включительно. И былали подсказка по СКО 30 января? Вопрос.
7. ФУНКЦИЯ ПЛОТНОСТИ ВЕРОЯТНОСТИ
В заключение остановимся на нормальном распределении, тесно связанным со средним значением случайной величины и среднеквадратическим отклонением.
Вначале ознакомимся с функцией плотности вероятности (ФПВ), обозначим ее через f(x). Пусть вероятность того, что непрерывная одномерная величина х на отрезке [a;b] равна P(a,b), тогда, исходя из f(x):
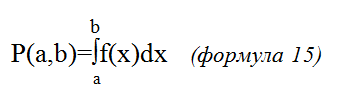
f(x) играет роль «плотности вероятности» в смысле «вероятности на единицу длины» для одномерной случайной величины х. Условно говоря, размерность f(x) – допустим, сантиметр или (если хотите), метр, в минус первой степени: см-1 или м-1.
∫ - знак интеграла, в данном случае, «определенного интеграла» от a до b.
Напомним, что определенный интеграл определяется (простите за тавтологию) следующим образом:
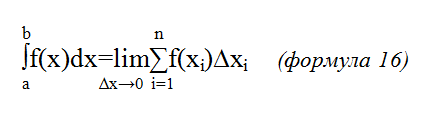
Отрезок [a;b] разбивается на n частей, длиной ∆xi каждая, внутри i-го промежутка берется xi. Далее, соответствующее значение функции f(xi) и умножается на ∆xi. Получаются площади, таких себе, маленьких прямоугольников, они суммируются в общую площадь. При ∆xi→0 (тогда, как правило, n→∞) выходим на определенный интеграл.
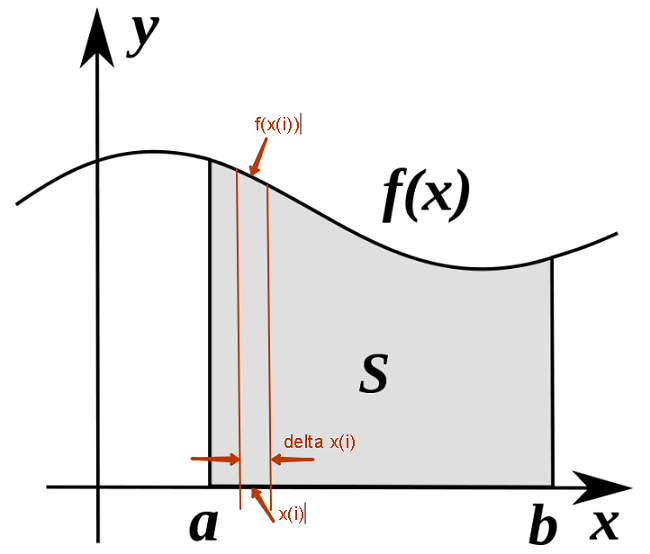
На рисунке – геометрическая интерпретация определенного интеграла. Вероятность P(a,b) из формулы 17 – площадь S светло серой фигуры.
для рисунка: xi = x(i), f(xi) = f(x(i)), ∆xi = delta x(i)
Очевидно, что на всей области определения аргумента х (примем от -∞ до +∞):
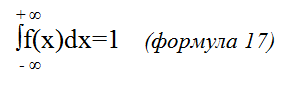
То есть, полная вероятность равна 1.
Для акций и прочих фининструментов эту геометрию можно интерпретировать так. Площадь S (вероятность P(a,b)) трактуется, как вероятность попадания стоимости ценной бумаги в интервал цен [a;b]. А формула 17 – говорит о том, что на всем множестве изменения цены, с вероятностью = 1, акция будет иметь какую-нибудь стоимость. Конечно, область определения цены инструмента лежит в два раза более узком теоретическом диапазоне (0;+∞).
Нормальным распределением (НР) называется распределение вероятностей, задаваемое функцией плотности вероятности, совпадающее с функцией Гаусса[16]:
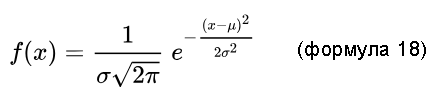
источник[16]
где:
μ – матожидание (среднее значение) случайной величины х, если μ – среднее арифметическое то, по тексту оно обозначалось, как <x>;
σ – среднеквадратичное отклонение.
Нормальное распределение также называется распределением Гаусса (гауссовым распределением) или распределением Гаусса-Лапласа.
Если μ=0, а σ=1, то нормальное распределение именуется стандартным НР.
График функции Гаусса (график НР) имеет вид:
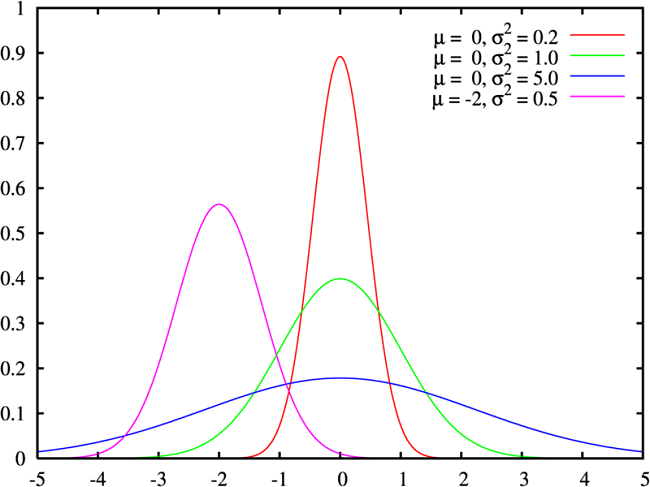
источник[16]
Зеленая кривая отвечает стандартному нормальному распределению.
В чем значение нормального распределения (НР)? Почему оно столь важно?
Согласно «центральной предельной теореме (теоремам)» теории вероятностей (ТВ), при увеличении числа измерений (идеально при n→∞) независимых (или, как математики осторожно говорят «слабо взаимозависимых») величин, их распределение стремится к нормальному. Это относится, как к стрельбе в тире, так и к любому природному или экономическому явлению. В том числе и ценовому спектру финансового инструмента.
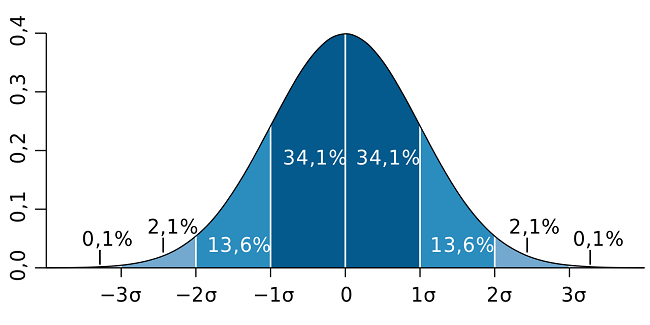
Иллюстрация «Правила трех сигм»[12]
Еще одним важным выводом ТВ для нормального распределения является «Правило трех сигм»[12]. Оно заключается в том, что с вероятностью 0,9973 значения нормально распределенной величины находятся в интервале (<x>-3σ; <x>+3σ).
(источник – статьи русскоязычной Википедии или авторский комментарий, если не оговорено иное)
- ↑ «Теория вероятностей».
- ↑ «Аксиоматика Колмогорова».
- ↑ «Колмогоров, Андрей Николаевич».
- ↑ «Случайное событие».
- ↑ «Случайный эксперимент».
- ↑ «Случайная величина».
- ↑ «Вероятностные разделы математики», СПб, 2001, цитируется по статье Википедии «Математическая статистика».
- ↑ «Вероятность».
- ↑ «Математическое ожидание».
- ↑ Среднее арифметическое величины <R>, принимающее n значений: R1, R2, ….. Rn, высчитывается, как (R1 + R2 + ….+ Rn)/n
- ↑ «Дисперсия случайной величины».
- ↑ «Среднеквадратическое отклонение».
- ↑ «Генеральная совокупность».
- ↑ https://finviz.com/
- ↑ https://finance.yahoo.com
- ↑ «Нормальное распределение»
ТВ – теория вероятностей
МО – матожидание, математическое ожидание
СКО – среднеквадратичное (среднеквадратическое, стандартное) отклонение, σ
ФПВ – функция плотности вероятности, f(x)
ЦБ – ценная бумага
FB – тикер акций Facebook
НР – нормальное распределение