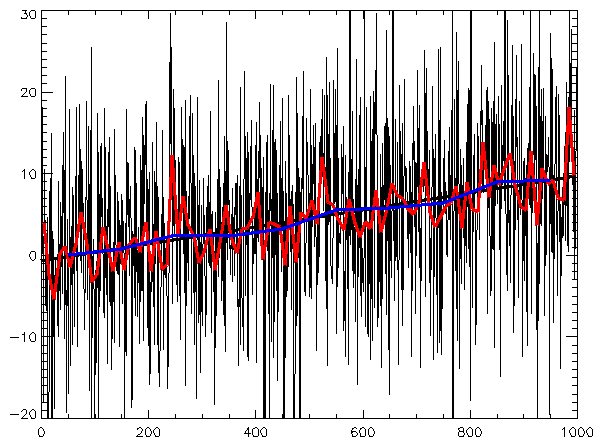
Вводный материал о временных рядах. Понятие, классификация, общие принципы исследования. Суть применения временных рядов для изучения биржевых трендов финансовых инструментов.

Содержание:

• Понятие временного ряда и цели его анализа
• Классификация временных рядов
• Базовые принципы прогноза
• Компоненты временного ряда
• Сглаживание. Скользящая средняя и медиана

       Скользящая средняя

       Медиана

• Подбор функции 

       Ряд Тейлора и ряд Маклорена

       Метод наименьших квадратов

• Интегрированный временной ряд и лаговый оператор
• Модели временных рядов. От простого к сложному

      Авторегрессионная модель (AR-модель)

      Модель скользящего среднего (MA-модель)

      Модель авторегрессии - скользящего среднего (ARMA-модель)

      ARIMA

      ARCH и GARCH

• Примечания и ссылки
• Используемые сокращения

Понятие временного ряда и цели его анализа

Временной ряд (далее по тексту ВР или, кратко, ряд) определяется как последовательность измерений, произведенных в неслучайные моменты времени. Другое наименование, применяемое для ВР – ряд динамики; для измерения временного ряда – уровень, отсчет (значение) на данный момент времени^[1].

Введение временной шкалы в явление ВР существенно отличает его от простой (случайной) выборки статистических данных. Ключевая особенность временного ряда – привязка значений (измерений) к соответствующим моментам времени. В изучении случайной выборки обычно не важна, а подчас, и вовсе не интересна подобная хронологическая взаимосвязь. 

Анализ временного ряда преследует две главные цели:

1. Определение его структуры (природы).
2. Прогноз будущих значений ряда на основе текущих и прошлых измерений.

Обе тесно взаимосвязаны. Решение первой задачи необходимо для построения математической модели ВР, ее корректной идентификации и формализации. Матмодель станет, своего рода, лабораторией  для исследования временного ряда и фундаментом для относительно точных (с допустимой нормой погрешности) предсказаний по ряду.

Структура любого ВР включает два сегмента: общий временной период с разбивкой на интервалы внутри него в которых (на концах) которых проводятся измерения (например, устанавливается котировка акции), и собственно, сами значения ряда (котировки ценной бумаги).

Вторая цель представляет особый интерес. В конечном счете, ради нее и реализуется первое направление, являющееся начальным, необходимым, но недостаточным этапом анализа. Прогноз -   экстраполяция значений ряда на будущий отрезок времени, используя исторический массив данных, пропущенный через механизм найденной матмодели.

Очевидно, что  для инвестора и трейдера методики изучения временных рядов имеют исключительную ценность . Их понимание, освоение и правильное применение в биржевой практике - залог успешных инвестиций и торговли финансовыми инструментами.

Классификация временных рядов

ВР различают по следующим признакам.

1. По временным параметрам.

1.1. Равноотстоящие и неравноотстоящие ряды.

В первом случае отметки времени, в которые фиксируются значения ВР, отстают друг от друга на одинаковые интервалы. Во втором - принцип равенства  интервалов не соблюдается.

1.2. Моментные и интервальные ряды.

Значения моментного ВР устанавливаются в отдельные, точечные моменты времени. В интервальных рядах работают уровни за определенные периоды. Это может достигаться, допустим, усреднением отсчетов по взятым интервалам. 

2. По размерности показателей (значений).

Одномерные и многомерные (двух-, трехмерные и т.д.) временные ряды.

3. По форме отображения (вида) отсчетов.

ВР могут содержать абсолютные, относительные и средние значения исследуемых показателей.

4. По полноте.

Полные и неполные ряды. В полных нет пропущенных значений, соответственно, в неполных ВР пропуски возможны.

5. По случайности отображаемого рядом процесса.

Случайные и детерминированные временные ряды. Случайный ВР - итог некоторого случайного явления. Детерминированный ряд может быть описан неслучайной (детерминированной) функцией^[2]. 

6. По наличию выделенной тенденции.

Стационарные и нестационарные ВР. Стационарные ряды характеризуются постоянством средних значений и дисперсий его величин. В нестационарных рядах прослеживается основная тенденция их эволюции. 

Базовые принципы прогноза

В целом, при изучении поведения временного ряда и построения его прогнозных оценок применяется  следующая последовательность действий.

1. Обнаружение закономерностей по ВР на прошлых (исторических) данных.

2. Конструирование функции (соотношений), способных максимально точно отразить выявленные на первом этапе трендовые тенденции. Отработка такой функции предоставит возможность оценить степень достоверности результатов начального этапа.

3. Экстраполяция найденных взаимосвязей на будущий период времени. Другими словами, попытка качественного предсказания уровней ряда в будущем. Математически “очень просто” - подстановка в трендовую формулу, найденную на этапе 2 будущих значений времени.

4. Сравнение прогнозных данных с текущими измерениями временного ряда. Отладка трендовой функции.

Далее, этапы 3 и 4 повторяются до достижении требуемой точности (удовлетворительности) прогноза.

Для построения заслуживающего доверия прогноза, временные параметры ряда должны отвечать нижеприведенным требованиям:

1. Равенство интервалов.
2. Фиксация значений ВР в аналогичных точках интервала (в начале, в конце, в середине и т.д.)
3. Непрерывность ряда.

Подобные условия вполне укладываются в структуру стандартного случайного эксперимента^[3].

Для временного ряда котировок акции, отраженного на графике ее курса, анализируются один и тот же таймфрейм^[4] , минута, пятиминутка, час и т.д. Значения берутся, как правило, по закрытию интервала, и каждому моменту времени должна отвечать своя котировка акции (допустим, bid, ask, (bid+ask)/2, цена последней сделки). 

Легко видеть, что согласно приведенной выше классификации ВР, для полноценного изучения максимально подходят равноотстающие полные ряды. В случае, когда отсутствуют данные за сравнительно небольшие отрезки времени, их можно заменить путем усреднения находящихся рядом известных уровней ВР.

Компоненты временного ряда

В первом приближении, любой ВР (как и иной объект “временного” анализа) представляется как комбинация двух составляющих: регулярной (систематической) и случайной (шум, белый шум^[5]). Для простоты, шум часто рассматривают, как некоторую погрешность, ошибку, искажающую проявление регулярной компоненты  временного ряда. Одна из ключевых задач в исследовании ВР - снижение (фильтрация) шума для выявления и идентификации систематической составляющей ряда, ответственной за его магистральный тренд. 

В свою очередь, регулярную компоненту ВР можно разложить на две части. Первая - постоянная величина, константа, вторая - линейная или нелинейная компонента, функция времени. Именно она  определяет тенденцию временного ряда. 

Неплохая наглядная аналогия подобной визуализации ВР просматривается в зависимости доходности отдельной акции от общей среднерыночной доходности (доходности фондового индекса) через β-коэффициент:

Безусловно, данная зависимость не является временным рядом, так как время не входит в нее, как независимая переменная и отсчеты по времени не производятся. В известном смысле, “роль” времени исполняет параметр R_I, доходность  выбранного фондового индекса. Но прочие составляющие - налицо. Постоянная компонента - коэффициент смещения α и случайная погрешность ε. 

Сглаживание. Скользящая средняя и медиана

К сожалению, не существует универсального способа обнаружения систематического ядра временного ряда, элемента, ответственного за формирование тренда, и, как следствие - создания абсолютно корректного прогноза поведения ВР. 

Один из широко используемых подходов - сглаживание ряда. Он заключается в той или иной методике локального усреднения значений, когда случайные (несистематические) составляющие способны компенсировать друг друга.

Скользящая средняя

Самая распространенная методика сглаживания - скользящая средняя. 

Скользящая средняя, скользящее среднее (Moving Average, MA) — общее название для семейства функций, “значения которых в каждой точке определения равны среднему значению исходной функции за предыдущий период”^[6]. 

MA можно строить разными способами. 

Базовая MA -  простое или арифметическое скользящее среднее (Simple Moving Average, SMA). SMA в момент времени t (SMAt) рассчитывается, как среднее арифметическое n значений ряда:

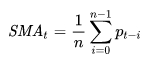
формула 2

где: p_t-i -  значение ряда в точке (в момент времени) t-i;

n именуется сглаживающим интервалом или шириной “окна”. 

Графическая интерпретация простого скользящего среднего приведена на рисунке^[6]:

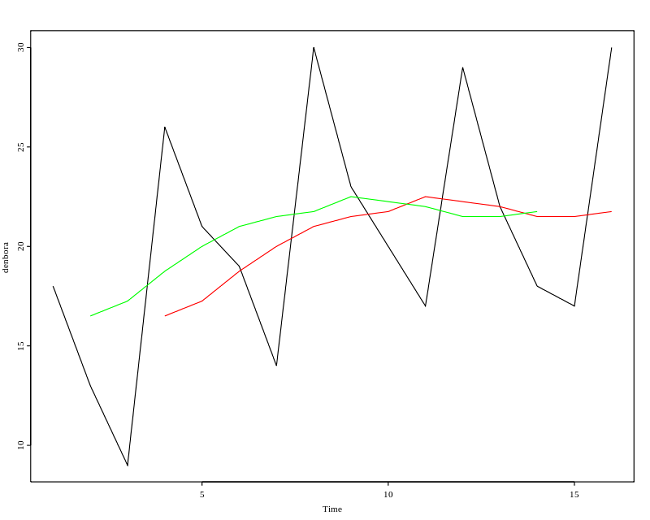
Здесь n=4, зеленая и красная линии - кривые SMA.

В простоте и ясности SMA заложены и ее недостатки. В частности, все значения SMA входит с одинаковым весом, а также - двойное реагирование на каждое слагаемое при перемещении от окна к окну. 

Вместе с тем, для временного ряда типична ситуация, когда одни его отсчеты более значимы, другие менее. Для корректного сглаживания такого ВР используют взвешенную скользящую среднюю (Weighted Moving Average, WMA).

WMA в момент t (WMAt):

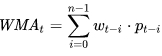
формула 3

где: p_t-i -  значение ряда в точке (момент времени) t-i;

w_t-i - нормированный вес уровня p_t-i.

Нормированные веса удовлетворяют традиционному условию:

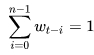
формула 4

То есть, их сумма по данному интервалу (окну) равна 1.

Медиана

Когда динамика временного ряда сопровождается большим количеством значительных выбросов (флуктуаций) внутри каждого (почти каждого) окна, более эффективным методом сглаживания будет медиана. Появление выбросов может быть связано, в том числе, и с большой относительной погрешностью измерений.

Напомним, что под медианой в статистике понимают “такое число <нечетной> выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него”^[7]. Например, медианой выборки (1,3,5,11,40) будет число 5. Число 40 можно считать выбросом. 

С четными выборками ситуация несколько сложнее. Допустим, для выборки (1,3,5,11) медианой допустимо считать любое число из интервала от 3 до 5 (средние “по росту” члены массива). Традиционно медиану здесь считают, как среднее арифметическое, то есть (3+5)/2=4. Таким образом, медиана (число) может и не входить в состав выборки.

Применение медианного сглаживания для неустойчивых рядов приведет к вычерчиванию более гладких, и, что важно, более надежных кривых, чем дало бы скользящее среднее. В силе медианного подхода заложена и его слабость. В тех рядах, где выбросы сравнительно  малы и/или редки медианное сглаживание строит неудобные зубчатые графики. Кроме того оно не позволяет задействовать веса.

Медианой и скользящим средним приемы сглаживания не исчерпываются. Существуют метод наименьших квадратов, взвешенных относительно расстояния, процедура отрицательного экспоненциально взвешенного сглаживания и целый ряд других более сложных методик.

Подбор функции

Исследование временного ряда значительно упрощается, если он имеет монотонный характер^[8]. Другими словами, он (возможно, после сглаживания) не убывает или не возрастает во времени на значительных периодах. В таком случае, прогноз будущих значений реализуется через подбор функции. Процедура приемлема, прежде всего, для детерминированных ВР.

Грубо это можно сделать применив линейную зависимость. Более тонкие, нелинейные подходы, используют экспоненциальную, логарифмическую функции, а также степенной полином (многочлен).

Ряд Тейлора и ряд Маклорена

Самый популярный полином, знакомый из начал математического анализа - ряд Тейлора и его частный случай, ряд Маклорена. Авторство первого приписывают английскому математику Бруку Тейлору (1685-1731)^[9]. Однако разложение функции в подобные ряды знали еще в Индии XIV века^[10]. Значительный след в теме оставили шотландец Джеймс Грегори (1638-1675)^[11] и великий Исаак Ньютон (1642-1727)^[12].

Исаак Ньютон, портрет Г. Кнеллера (1689)^[12]

Колин Маклорен, шотландский математик, работал чуть позже, ближе к середине XVIII века (годы жизни 1698-1746)^[13].

Разложение функции f(z) в бесконечный ряд Тейлора имеет вид:

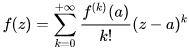
формула 5

где: f^k(a) - k-ая производная функции f(z) в некоторой точке "а".

Безусловно, выполнимость такого разложения предполагает взятие производной от функции любого порядка на ее области определения. В общем случае, ряд Тейлора имеет область (радиус) сходимости в районе точки “а”. Радиус сходимости R может быть вычислен с помощью формулы Даламбера. В частности, для экспоненты e^x он равен бесконечности. Возможность разложения функции в ряд Тейлора  является критерием ее аналитичности^[14]. 

В случае конечного (n) числа членов ряда Тейлора работает формула Тейлора:

f(x)=P_n(x)+Q_n(x), формула 6.

Здесь:

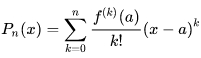
формула 7

n-ая частичная сумма ряда Тейлора для f(x). 

Q_n(x) - остаточный член, своего рода, погрешность разложения функции рядом Тейлора. Очевидно, Q_n(x)→0 при n→∞.

На практике применяют частный случай ряда (формулы) Тейлора для а=0. Такой ряд именуется рядом Маклорена:

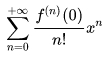
формула 8

Приведем два распространенных варианта ряда Маклорена.

Разложение экспоненты:

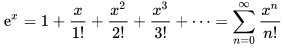
формула 9

и натурального логарифма (ряд Меркатора):

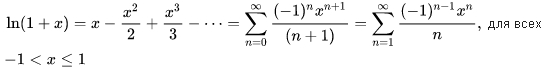
формула 10

Метод наименьших квадратов

Оптимизировать трендовую функцию полезно через метод наименьших квадратов^[15]. 

Запишем временной ряд в виде: 

y_t=f(x_t,b)+ε_t

где:y_t - значение ВР для t=1,.... ,n;

f - подобранная (оптимизируемая) функция, от некоего аргумента x_t (например, комбинации предшествующих значений ряда y_t-1, y_t-2 и т.д.);

b - параметр оптимизации;

ε_t - белый шум. 

Суть метода наименьших квадратов заключается в минимизации суммы квадратов разницы между y_t и f(x_t,b) через подгон параметра b:

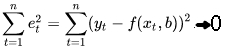
формула 11

Интегрированный временной ряд и лаговый оператор

Особый интерес для алготрейдера представляют нестационарные ВР. Биржевые тренды ценных бумаг и прочих финансовых активов имеют именно такой характер. Среди нестационарных рядов принято выделять класс интегрированных временных рядов.

Интегрированный ВР трактуется, как “нестационарный временной ряд X_t, разности некоторого порядка которого являются уже стационарным временным рядом”^[16]. При этом, требуется, чтобы ряды, составленные из разностей меньшего порядка, по-прежнему, имели нестационарный вид. Отсюда логично следует другое название интегрированного ВР - разностно-стационарный ряд или DS-ряд (англ. Difference Stationary). Принятая запись для интегрированного ряда k-го порядка: X_t~I(k).

Под разностью k-го порядка понимают процедуру, когда из каждого i-го члена ВР вычитают (i-k)-ый член. Например, разность третьего порядка (k=3), предполагает, что из четвертого элемента ряда будет удален первый элемент (4-3=1), из пятого - второй (5-3=2), из шестого - третий (6-3=3) и т.д. В таком случае, новый ВР начнется с разности четвертого и третьего члена исходного ряда, так как для нее первой будет выполнено неравенство i-3>0.

Подобное вычитание может, во-первых, вскрыть неявную периодическую зависимость ВР. И, во-вторых - перейти от нестационарного ряда к ряду стационарному. В последнем случае и имеем интегрированный временной ряд.

Наглядно разности (иногда говорят “конечные разности”) k-го порядка показывает лаговый оператор (оператора смещения) L^[17]. 

Лаговый оператор k-го порядка вводится так:

L^kX_t=X_t-k, формула 12

Оператор L “смещает” член ряда X_t в X_t-k: X_t→X_t-k.

Тогда разность k-го порядка Δ^kX=X_t-X_t-k=X_t-L^kX_t=(1-L^k)X_t.

Разность первого порядка: Δ¹X=ΔX=X_t-X_t-1=(1-L¹)X_t=(1-L)X_t.

Второго порядка Δ²X=X_t-X_t-2=(1-L²)X_t и т.д.

Разность нулевого порядка не сдвигает члены ряда: L⁰X_t=X_t.

Модели временных рядов. От простого к сложному

В заключительном разделе перечислим в самом общем виде несколько актуальных моделей временных рядов, используемых в современных торговых алгоритмах и стратегиях. 

Авторегрессионная модель (AR-модель)

Авторегрессионная модель, Autoregressive Model, кратко AR-модель, предполагает линейную зависимость члена временного ряда в заданный момент времени от предыдущих его значений^[18] (с латинского regressus — возвращение, обратное движение):

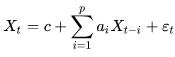
формула 13

где: c - константа, a_i - авторегрессионные коэффициенты, ε_t - шум.

Число членов в сумме - p определяет порядок авторегрессионной модели. Таким образом, формула 13 описывает авторегрессионный процесс порядка p или, кратко, AR(p)-процесс.

Процесс первого порядка,  AR(1)-процесс представляет знаменитое случайное блуждание:

X_t=c+aX_t-1+ε_t, формула 14

Модель скользящего среднего (MA-модель)

Модели скользящего среднего, Moving Average Model, кратко MA-модели q-го порядка, MA(q) отвечает следующее соотношение^[19]:

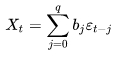
формула 15

где: b_j - коэффициенты скользящего среднего (b₀=1) или параметры модели, ε_t  - шум.

MA-модель нулевого порядка, MA(0) представляет собой просто белый шум: X_t=ε_t.

На практике обычно применяют MA-модель первого порядка, MA(1):

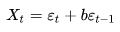
формула 16

Модель авторегрессии - скользящего среднего (ARMA-модель)

Модель авторегрессии — скользящего среднего (AutoRegressive Moving-Average Model, ARMA) объединяет обе модели (AR+MA=ARMA) в одно целое^[20]:

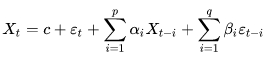
формула 17

Обозначения в формуле 17 для ARMA те же самые, что в формулах 13, 15 для AR- и MA-моделей соответственно. Формула 17 характеризует ARMA-модель с двумя параметрами p и q - модель ARMA(p,q).

Комбинация AR- и MA-модели в единую ARMA позволяет  более тонко смоделировать временной ряд, используя сильные стороны обеих методик. ARMA может трактоваться, как “линейная модель множественной регрессии”. Линейная часть заложена AR-компонентой, а влияние белого шума отражено MA-составляющей.

ARIMA

Еще более сложная конструкция известна, как “интегрированная модель авторегрессии - скользящего среднего”^[21],  AutoRegressive Integrated Moving Average, кратко ARIMA (ровно в середину аббревиатуры ARMA добавили букву I=Integrated). Статистики именуют ее иногда также, как модель (методологию) Бокса-Дженкинса.

ARIMA адаптирует базовую ARMA под исследование интегрированных (разностно-стационарных) временных рядов и имеет уже три параметра. К p и q от ARMA прибавляется d - порядок разности интегрированного ряда, то есть, номер конечной разности, при которой нестационарный ряд переходит в стационарный. ARIMA (p,d,q) - это модель ARMA (p,q), примененная на разнице ряда d-го порядка. 

Математика ARIMA (p,d,q) выглядит так:

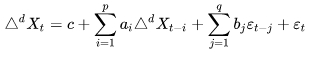
формула 18

где: с, a_i, b_j, ε_t - величины, уже определенные в формуле 17 для ARMA-модели;

Δ^dX -  разность d-го порядка по ряду X.

ARCH и GARCH

Относительно недавно исследователи финансовых нестационарных временных рядов взяли на вооружение модели линии ARCH и GARCH. Что стоит за этими англоязычными аббревиатурами?

В основе данных методик лежит модель авторегрессионной условной гетероскедастичности, AutoRegressive Conditional Heteroscedasticity, кратко ARCH^[22]. Трудно произносимое слово “гетероскедастичность” отражает суть модели. В статистике гетероскедастичность - такое свойство ряда, при котором его значения неравномерно (с неустойчивой дисперсией) располагаются вдоль линии выявленного магистрального тренда на всем диапазоне анализа^[23]. Приставка “гетеро” с греческого означает  “ино-”, “разно-”, “различно-”^[24].

ARCH-модели предполагает, что условная (по предыдущим значениям) дисперсия гетероскедастичного ряда зависит от самих прошлых уровней ряда. “Отцом” ARCH считают американца Роберта Энгла, Robert Fry Engle III. В 1982 году он предложил модель, в которой дисперсия временного ряда может быть обусловлена его прошлыми значениями. В 2003 году Р. Энгл был удостаивается Нобелевской премии по экономике с формулировкой “за разработку методов анализа экономических временных рядов с временными изменениями”^[25].

 

Роберт Энгл, 2017 г.^[25]

Согласно гипотезе Р. Энгла, условная дисперсия в рамках модели ARCH q-го порядка,  ARCH(q) описывается следующим образом:

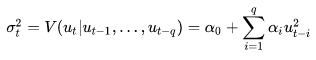
формула 19

где: α₀, α_i - параметры модели;

u_t - значения членов ряда.

ARCH показала свою эффективность  при интерпретации кластеризации волатильности на фондовом, валютном и прочих финансовых рынках, когда периоды высокой волатильности сменяются периодами низкой, при том, что среднюю долгосрочную волатильность можно оценивать, как относительно неизменный фактор.

В 1986 году датчанин Тим Боллерслев, Tim Peter Bollerslev^[26] модернизировал ARCH в GARCH. Приставленная впереди аббревиатуры буква G обозначает Generalized. Generalized ARCH (GARCH), по-русски - обобщенная ARCH-модель. 

Т. Боллерслев сделал вполне разумное и логичное предположение, о том, что для корректного прогноза отдельных неустойчивых временных рядов в формулу 19 для ARCH-модели полезным будет введение компоненты, отвечающей за предыдущие условные дисперсии.

Оценка условной дисперсии модели GARCH порядка (p,q) - GARCH(p,q)-модели имеет вид: 

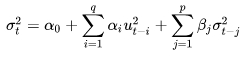
формула 20

где: α₀, α_i и u_t уже введены в формуле 19 для ARCH;

σ_t-j - прошлые значения условных дисперсий;

β_j - коэффициенты (параметры) модели.

Необходимое условие стационарности ряда, согласно GARCH записывается так:

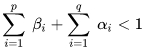
формула 21

Линейка актуальных моделей исследования временных рядов в алготрейдинге отнюдь не ограничивается приведенными выше примерами. Алгоритмы используют их комбинации и усовершенствованные варианты.

В частности, на слуху симбиоз ARIMA+GARCH и целое семейство, собственно “GARCH-ей” адаптированных для тех или иных целей: GARCH-M, асимметричные GARCH, в том числе, EGARCH, AGARCH, TGARCH, GJR-GARCH и многие другие.

Владимир Наливайский

 

В изложении использован материал «Анализ временных рядов» портала StatSoft 

Источник изображения на заставке статьи - Википедия^[1]

Примечания и ссылки (источник – Википедия/Wikipedia если не оговорено иное)

1. “Временной ряд”.
2. Функция является детерминированной, если для одного и того же набора входных значений она возвращает одинаковый результат, “Чистота функции”.
3. “Случайный эксперимент”.
4. Таймфрейм (time-frame) или торговый период — интервал времени, используемый для группировки котировок при построении элементов ценового графика, “Таймфрейм”.
5. Белый шум - стационарный шум, спектральные составляющие которого равномерно распределены по всему диапазону задействованных частот, “Белый шум”.
6. “Скользящая средняя”.
7. “Медиана (статистика)”.
8. “Монотонная функция”.
9. “Тейлор, Брук”.
10. “Ряд Тейлора”.
11. “Грегори, Джеймс”.
12. “Ньютон Исаак”.
13. “Маклорен, Колин”.
14. “Аналитическая функция”.
15. “Метод наименьших квадратов”
16. “Интегрированный временной ряд”.
17. “Лаговый оператор”.
18. “Авторегрессионная модель”.
19. “Модель скользящего среднего”.
20. “Модель авторегрессии - скользящего среднего”.
21. “ARIMA”.
22. “Авторегрессионная условная гетероскедастичность”.
23. По информации портала Loginom.
24. “Гетеро-”.
25. “Энгл, Роберт”.
26. ”Tim Bollerslev”.

 

Используемые сокращения

ВР - временной ряд

MA - Moving Average, скользящая средняя, скользящее среднее

SMA - Simple Moving Average, простое или арифметическое скользящее среднее

WMA - Weighted Moving Average, взвешенное скользящее среднее

AR-модель - AutoRegressive Model, авторегрессионная модель

MA-модель - Moving Average Model, модель скользящего среднего

ARMA - AutoRegressive Moving-Average Model, модель авторегрессии — скользящего среднего

ARIMA - AutoRegressive Integrated Moving Average, интегрированная модель авторегрессии - скользящего среднего

ARCH - AutoRegressive Conditional Heteroscedasticity, модель авторегрессионной условной гетероскедастичности

GARCH - Generalized ARCH, обобщенная ARCH-модель.