Вводный материал о процессе случайного блуждания. Базовые определения и доступное объяснение сути явления на отдельных примерах из физики и математики. История вопроса и роль выдающихся ученых. Статья продолжает серию публикаций сайта по основам теории вероятностей и математической статистики и их приложениям в инвестиционной деятельности.

Содержание:

• Введение. Русские математики Андреи Марковы
• Немарковский процесс
• Броуновское движение
• Марковский процесс
• Случайное блуждание
• Примечания и ссылки

Введение. Русские математики Андреи Марковы

Русская математическая школа – одна из виднейших в мире. Ведет свое начало с 1725 г., сразу после учреждения Петербургской (Императорской) академии наук, предшественницы АН СССР и современной Российской академии наук (РАН). Из 22 профессоров и адъюнктов, приехавших в Россию по приглашению Екатерины I, было 8 математиков, включая знаменитых швейцарцев-базельцев Леонарда Эйлера и Даниила Бернулли. Бурно развивающаяся в те годы Россия представлялась весьма привлекательным местом работы для специалистов такого уровня.

Эйлер прибыл в Петербург в мае 1727 года^[1] и «отслужил» в Императорской академии два периода: с 1727 по 1741 и с 1766, вплоть до смерти в 1783-м. Почти 40 лет. От Эйлера принято отсчитывать историю математики в России.

Дореволюционный этап изобилует именами «математических звезд первой величины»: Остроградский, Лобачевский, Чебышев, Ляпунов, Стеклов.

Достойное место в плеяде российских математиков начала прошлого века занимает Андрей Андреевич Марков (1856-1922). Интересы Маркова сосредоточились на теории чисел, математическом анализе и теории вероятностей^[2].

 

А.А. Марков (старший) ^[2]

 

Андрей Андреевич был не только выдающимся математиком. Масштаб личности проявлялся по многим направлениям. Сильный, уровня мастера спорта, шахматист. Активно играл по переписке. Шахматный архив» Маркова состоит из более, чем 1500 писем.

Стойкая общественная позиция. В 1901 г. А.А. Марков резко осудил решение Синода об отлучении Льва Толстого от церкви, а в 1912-ом он просил Синод сделать такое же действие по отношению к нему самому. Духовная консистория Санкт-Петербурга «пошла навстречу академику».

В 1903 году у 45-летнего (!) Маркова и его супруги рождается сын. Имя родители долго не выбирали. Конечно, Андрей. А сын долго не выбирал профессию. Безусловно, математик.

Андрей Андреевич Марков-младший (1903-1979) – видный представитель уже советской математической школы. Отличился фундаментальными трудами в области топологии, динамических систем, теории алгоритмов и конструктивной математики^[3].

Нелегко сравнивать вклад в науку отца и сына, вклад двух Андреев Марковых. Они разрабатывали разные разделы математики. Для теории случайных (стохастических) процессов трудно переоценить значение исследований Маркова-старшего. Ряд понятий из мира случайных событий носят имя русского математика-шахматиста. Наивысшая степень признательности заслуг любого ученого. Повыше Нобелевской и Абелевской премий^[4].

Немарковский процесс

Прежде всего, с именем Маркова-старшего связывают два типа случайных процессов.

Начнем с отрицательной частицы «не».

Немарковский процесс – «случайный процесс, эволюция которого после любого заданного значения времени зависит от эволюции, предшествовавшей этому моменту времени»^[5].

Можно сказать, что немарковский процесс имеет память. Последующие события, происходящие в нем, помнят предыдущие. Будущее формируется в прошлом: «от характера эволюции процесса в прошлом зависят его статистические характеристики в будущем».

Броуновское движение

Классический пример немарковского процесса в физике – броуновское движение^[6].

Броуновское движение – «беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа»^[7]. Броуновское движение – подтверждение непрерывного теплового перемещения атомов и молекул жидкости или газа.

Для того, чтобы увидеть броуновское движение в тепловую среду помещают броуновскую частицу – тело, линейным размером менее 3 микрон. Под действием постоянно налетающих на нее атомов и молекул, броуновская частица хаотически перемещается в среде. Обычно наблюдение проводится под микроскопом. Более крупные тела (от 5 микрон) на толчки соседей уже не реагируют.

Броуновские прыжки иллюстрирует картинка из книги Перрена «Les Atomes»:

 

Движение трех броуновских (коллоидальных) частиц под микроскопом

 

Радиус частицы 0,53 мкм, временной интервал между точками 30 секунд, шаг сетки 3,2 мкм.

В теории броуновского движения отметился тогда еще совсем молодой Альберт Эйнштейн. В свой самый плодотворный 1905-ый год, наряду с основами теории относительности и квантовой природы фотоэффекта, скромный 26-летний служащий Бернского патентного бюро публикует статью под длинным, возможно излишне подробным (но так тогда было принято) названием «О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты»^[9].

Именно за работы по статистической физике, в том же 1905-ом, Эйнштейн получает звание доктора философии, аналог нашего кандидата наук. Первое, пусть небольшое признание его вклада в науку.

 

А. Эйнштейн в патентном бюро, Берн, 1905 г.^[9]

 

Тема броуновского движения – одна из любимых становящегося на ноги крупнейшего физика-теоретика XX века. Он возвращается к ней в следующем 1906 году, выпуская материал большей емкости, но с меньшим заголовком «К теории броуновского движения». Броуновское движение стало прологом к таким вершинам Эйнштейновского гения, как теория флуктуации, квантовая теория теплоемкости и квантовая статистика Бозе-Эйнштейна.

Формулы А. Эйнштейна для числовой интерпретации броуновского движения элегантны и лаконичны, в отличие от наименований некоторых его статей. В стиле великого физика, как легендарное соотношение для полной энергии E=mc².

Приведем две.

Первая связывает квадрат смещения броуновской частицы вдоль любого направления с периодом времени, за который это смещение происходит:

Вторая описывает вращательное движение частицы и дает зависимость среднего квадрата угла поворота, относительно произвольной оси, от времени:

Почему броуновское движение немарковский процесс?

Проходя участки траектории, частица увлекает за собой ближайшее окружение, и оно начинает по-новому влиять на взвешенное тело. Следовательно, движение броуновской частицы обусловлено ее предыдущим состоянием, ее ближайшим прошлым. Прослеживается четкая связь между прошлым, настоящим и будущим.

Марковский процесс

Марковский процесс – «действие с амнезией».

Марковский процесс – «случайный процесс, эволюция которого после любого заданного значения времени не зависит от эволюции, предшествовавшей этому моменту времени, при условии, что значение процесса в этот момент фиксировано; «будущее» процесса не зависит от «прошлого» при известном «настоящем»^[8].

Первая половина определения один в один повторяет толкование немарковского процесса, приведенное выше, плюс отрицательная частичка «не», переводящее немарковский признак в марковский.

Существуют вариации трактовки марковских процессов. Например, «процесс, следующее состояние которого зависит вероятностно только от текущего состояния». Или: «будущее марковского процесса зависит от «прошлого» лишь через «настоящее» (А.Д. Вентцель).

Марковский процесс, у которого пространство состояний имеет дискретный характер (не более, чем счетно) носит название марковской цепи.

Понятие «марковости» в случайном процессе было заложено А.А. Марковым-старшим в 1907 году.

Случайное блуждание

Самая наглядная иллюстрация марковского процесса – случайное блуждание.

Случайное блуждание понимается, как «математическая модель процесса случайных изменений — шагов в дискретные моменты времени». При этом предполагается, что изменение на каждом шаге не зависит от предыдущих шагов и от времени^[10].

Традиционная картинка для иллюстрации случайного блуждания – точка, двигающаяся вдоль оси в одном из двух направлений, шагами одинаковой длины. Курс определяется подбрасыванием монеты. Орел – положительное направление вдоль оси, решка – противоположное, отрицательное направление. Подобное движение именуется одномерным дискретным случайным движением.

Математически процесс укладывается в такое соотношение:

источник^[10]

Точка перемещается из начального состояния Y₀ вдоль оси Y. Монета подбрасывается n раз. Вероятность выпадения орла на i-ом броске: p_i. При орле точка сдвигается на единицу вверх. Вероятность выпадения решки на i-ом броске: q_i=1- p_i. В случае решки точка сдвигается на единицу вниз. Итог n бросков монеты – точка оказывается на ординате Y_n.

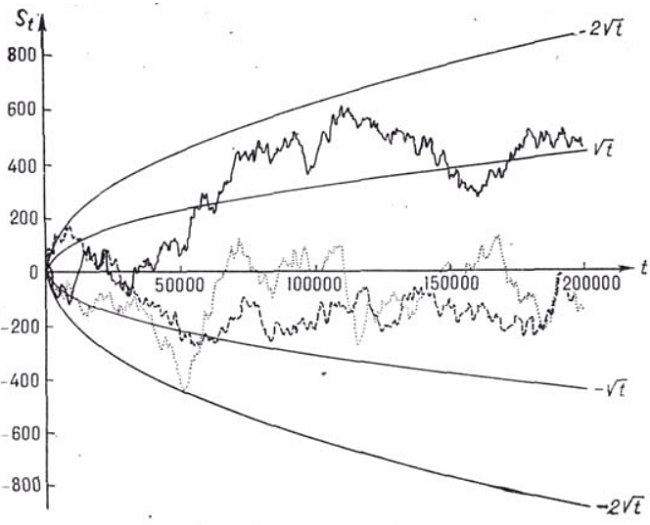
Ниже приводится часто цитируемые в сети графики восьми одномерных случайных блужданий (ось X – число бросков монеты):

 

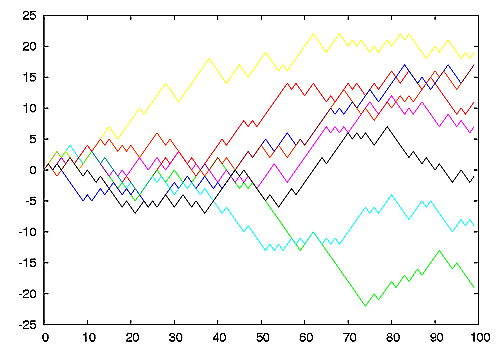
источник^[10]

 

Одномерный случай случайного блуждания легко обобщается на многомерный.

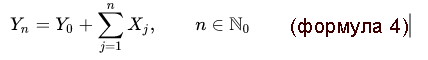
источник^[10]

Здесь X_j, Y₀, Y_n … – s-мерные координаты (изменения координат) случайно блуждающей точки. s=2 (плоскость), s=3 (трехмерное пространство), s=4 (четырехмерное пространство), … s=u (u-мерное пространство).

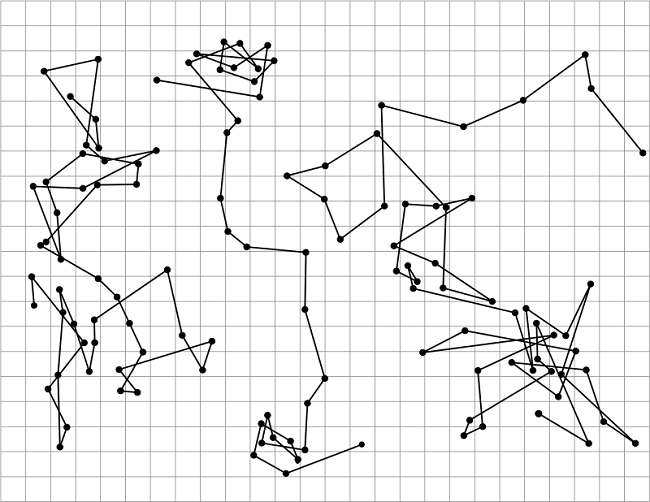
Представление о двумерном варианте дает следующий рисунок:

 

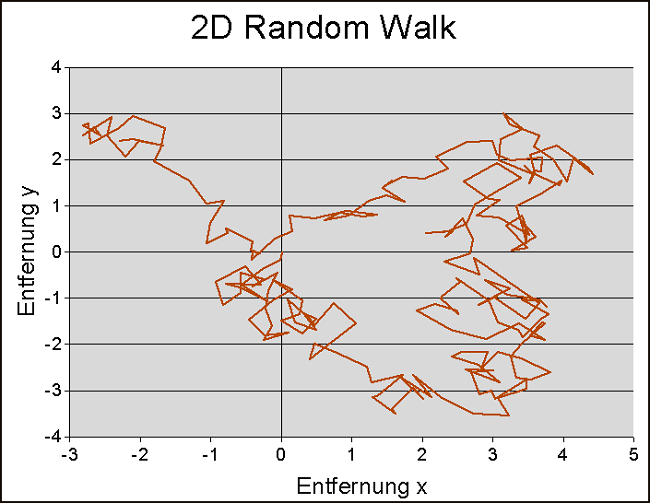
источник^[10]

 

Процесс занял 229 шагов, длина шага +0,5/-0,5. Для каждого шага монету надо бросать дважды или генерировать два случайных числа иным способом.

Гипотеза случайного блуждания на финансовых рынках и смежные с ней вопросы будут изложены в очередной статье рубрики.

 

Владимир Наливайский

 

Примечания и ссылки (источник – Википедия, если не оговорено иное)

1. «Леонард Эйлер»
2. «Марков, Андрей Андреевич, старший»
3. «Марков, Андрей Андреевич, младший»
4. Абелевская премия – премия по математике, названная в честь норвежского математика Н.Х. Абеля. Считается ближайшим аналогом Нобелевской премии (Нобелевская премия по математике не присуждается)
5. «Немарковский процесс»
6. Некоторые источники (см.^[8]) сообщают, что есть попытки трактовать броуновское движение, как вид марковского процесса
7. «Броуновское движение»
8. «Марковский процесс»
9. «Эйнштейн, Альберт»
10. «Случайное блуждание»