Вводный текст о математическом моделировании и методе Монте Карло.

 СОДЕРЖАНИЕ:

ВВЕДЕНИЕ. Гримальди, налоги и казино
1.  Математическое моделирование. Определение и классификация
2.  Имитационное моделирование
3.  Из истории метода Монте Карло
4.  Суть метода Монет Карло на примерах из занимательной математики
4.1. Французский граф, капитан и число π
4.2. Вычисление определенного интеграла
Примечания и ссылки
Используемые сокращения

ВВЕДЕНИЕ. ГРИМАЛЬДИ, НАЛОГИ И КАЗИНО

8 января 1297 года.

Франческо (Франсуа) Гримальди, по прозвищу «Хитрец», переодетый монахом, постучал в ворота крепости Монако^[2]. За его спиной стояла группа рослых людей в рясах. Им открыли, отряд вошел внутрь, «монахи» выхватили спрятанные под одеяниями мечи, и с боем заняли крепость.

С этого дня ведется отсчет правления княжеской династии генуэзцев Гримальди в Монако. За более, чем 700-летнюю историю Гримальди и управляемое им государство знавали разные времена. Сейчас Монако – синоним роскоши, блеска и безусловного успеха. Но так было не всегда.

В 1815-60 гг. княжество находилось под протекторатом Сардинского королевства^[3]. Не лучшие годы для Монако. Не самые богатые, сытые и благополучные. В 1848 году два города Ментон и Рокбрюн, объявили о своей независимости от Гримальди^[4]. Если бы «свободолюбивые» Ментон и Рокбрюн просто ушли, то и Бог с ними. Но они, неблагодарные, хлопнули дверью, «прихватив деньги» – налоги, которые отказались платить в пользу потомков «Хитреца» Франческо.

Серьезный удар. «Мятежные» города неплохо зарабатывали на торговле оливковым маслом и фруктами. Финансовые потери Гримальди после их бегства были ощутимы. Exit по-монакски образца середины XIX века усилил и без того, мягко говоря, сложное финансовое положение правящей династии. Она находилась в шаге от банкротства.

«Кто виноват» понятно, но вот: «Что делать?»

Монако – маленький кусочек каменистого средиземноморского побережья. Ни нефти и газа (да и кому они были бы нужны в 1848 г.?), ни золота, ни алмазов. Правящий принц Флорестан I совсем загрустил. Но у него было «сокровище». Жена. Не всегда супруга может помочь мужу (тем более, целому княжеству) так, как это сделала принцесса Каролина. Но Флорестану и Монако повезло.

Принцесса Каролина, Marie Caroline Gibert de Lametz (1793-1879)^[5]

Не то, чтобы Каролина была женщина с богатым приданым. Совсем нет. В прошлом французская театральная актриса. Какие деньги?

Но Каролина обладала нечто большим, чем капиталом во франках. У нее были креативность одаренного режиссера-постановщика и предприимчивость, помноженная на бульдожью деловую хватку, жесткого бизнесмена. И еще она отлично знала человеческую природу и маленькие человеческие слабости.

Идея национального спасения, выдвинутая Каролиной, умещалась в короткое слово из шести букв – «Казино», Casino.

История о том, как бывшая актриса создала с нуля, на камне и песке (буквально, это не гипербола) будущую легенду азартного бизнеса, первый номер среди игровых залов планеты, заслуживает отдельной статьи, а может быть и целого романа. Страсти вокруг Casino de Monte-Carlo, на этапе его становления бушевали нешуточные. Они вполне достойны пера Виктора Гюго и Оноре де Бальзака, великих современников-соотечественников Каролины. Жаль, что те не взялись за такой труд.

Первое казино Монте-Карло открывается 14 декабря 1856 года на Villa Bellevu. На свое теперешнее место, в здание по проекту парижского архитектора Gobineau de la Bretonnerie на Les Spelugues (англ. The Caves), оно переехало в 1863 г.

Сейчас «Монте-Карло» стало, во многом, именем нарицательным, давшим (помимо разным казино Монако) названия многим шикарным вещам, явлениям, кинокартинам и пр. Трасса Формулы-1, марки сигарет и автомобиля, культовые фильмы «Бондианы»…

А еще Монте-Карло широко известно среди математиков, физиков, экономистов и финансистов, которые могли никогда и не быть в Монако и не интересоваться его бурной историей и индустрией азарта.

Имя района карликового княжества и его казино присвоено знаменитому имитационному методу в математическом моделировании – методу Монте Карло (ММК).

1.  МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ. ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ

Процесс познания реальности неизменно требует математики. Будь то физика, химия, молекулярная биология, новейшие методы в медицине, а также социология и экономика, все эти дисциплины, в той или иной степени, используют математический аппарат разной сложности. Взрывное развитие компьютерных технологий вооружило исследователей и мощными численными приемами.

Математический метод изучения, систематизации и прогнозирования предполагает построение математической модели. Цель – замена реального объекта его теоретической, математической моделью (матмоделью, ММ) или, другими словами, динамической системой.

Обычно, понятия «матмодель» и «динамическая система» считаются тождественными. Иногда говорят, что данная система имеет ту или иную математическую модель, применяющую свой вид матаппарата.

Связь между матмоделью и реальным объектом устанавливается с помощью цепочки гипотез, идеализаций и упрощений^[6}.

Конечно, никакой ученый не сможет на 100% познать ни одно природное явление, «трудно быть Богом»^[7]. Но он в силах «прокачать» оптимальную матмодель, максимально приблизив ее к реальности. И, самое главное, что требуется от любой науки, теории и методики – предсказать поведение реального объекта в будущем.

Создание и исследование математической модели получило название математического моделирования.

Формальные классификации ММ строятся по принципу дихотомии^[8].

1) Линейные и нелинейные ММ.

В линейной динамической системе отклик системы на сумму воздействий равен сумме откликов на каждое воздействие^[9]. В нелинейной системе протекают процессы, описываемые нелинейными дифференциальными уравнениями^[10].

2) Сосредоточенные и распределенные ММ.

Динамические системы, использующие конечное число обыкновенных дифференциальных уравнений, именуются сосредоточенными или точечными. Сосредоточенным ММ присуще конечное число степеней свободы и входных данных.

Системы, моделируемые с помощью диффуравнений в частных производных, интегральных уравнений и обыкновенных уравнений с запаздывающим аргументом, называются распределенными системами. Число степеней свободы распределенной ММ бесконечно и требует бесконечное число данных для определения своего состояния.

Одна и та же матмодель в различных условиях или на разных стадиях может быть, как сосредоточенной, так и распределенной.

3) Детерминированные и стохастические ММ.

Детерминированное матмоделирование имеет место, когда протекающие в системе процессы детерминированы, другими словами, в ней исключены случайные воздействия. Напротив, стохастические динамические системы предполагают случайные, с той или иной степенью вероятности, события.

4) Статические и динамические ММ.

Статическая модель отображает объект только в конкретный момент, динамическая – на протяжении некоторого отрезка времени.

5) Дискретные, непрерывные и дискретно-непрерывные ММ.

Дискретные матмодели описывают процессы дискретного характера, в непрерывных – объекты (величины) изменяются непрерывно. Дискретно-непрерывные ММ представляют смешанный вариант, предусматривающий оба типа протекания явлений.

2.  ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

Один из видов стохастических динамических моделей – имитационная ММ.

«Имитационная модель — логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта»^[11].

В имитационном моделировании (simulation modeling) предмет исследования заменяется системой, над которой проводятся эксперименты для получения информации о поведении реального объекта при наборе определенных условий. Такая система многократно, возможно, тысячи и десятки тысяч раз, прогоняется на различных входных данных с помощью вычислительных машин. Набирается устойчивая статистика случайных, вероятностных состояний модели. Итог – усреднение полученных результатов.

Отработка ММ с помощью экспериментов и опытов называется имитацией. Естественное, действительное протекание процессов заменяется на их математическую симуляцию. Современный уровень компьютерных технологий позволяет все чаще и достаточно успешно заменять природу в естественных науках и финансово-экономической сфере.

Имитационное моделирование критично необходимо в тех системах, где создание аналитических, т.е. полностью связанных классической математикой, моделей невозможно или подобная аналитика приводит к неустойчивым решениям. Другой причиной использования имитационных ММ может быть их относительная дешевизна и доступность. Наконец, имитаторы незаменимы для прогнозирования поведения сложных систем во времени.

Из вышесказанного очевидно, что имитационное моделирование оптимально для алгоритмической торговли финансовыми инструментами.

Различают три вида имитационного моделирования (ИМ).

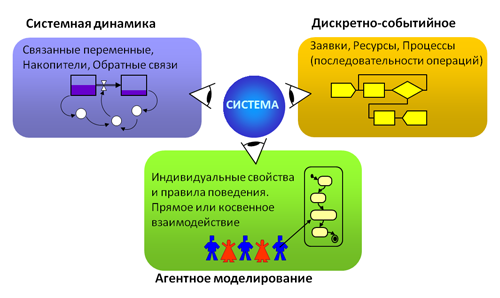
Три подхода в имитационном моделировании^[11]

1) Дискретно-событийное ИМ, Discrete-event simulation, DES^[12].

Самое распространенное направление в ИМ. Основано Джеффри Гордоном (1924-1989) в 1960-х годах.

Дискретно-событийное ИМ описывает функционирование системы, как некую хронологическую цепочку событий. Каждое такое событие происходит в определенное время и фиксирует новое состояния системы. Дискретно-событийное ИМ может иметь, как детерминированный, так и стохастический характер.

Дискретно-событийная модель включает три составляющие: часы, список событий и генератор случайных чисел (ГСЧ).

Данный вид ИМ получил широкое признание в логистике, наладке технологических систем и обслуживании больших клиентских групп (ритейл и пр.).

2) Системная динамика.

Тип ИМ, в котором между параметрами системы выстраиваются графические диаграммы глобальных причинно-следственных связей во времени. Данные зависимости зашиваются в модель, которая и подвергается имитационному компьютерному моделированию. Впервые метод системной динамики был предложен в 1950-х гг. американским системологом Джеем Райтом Форрестером из Массачусетского технологического института.

Системная динамика плодотворно применяется на моделях бизнес-процессов, в частности, при маркетинговых исследованиях выводимого на рынок продукта, развитии городских агломераций, при биологических, экологических и эпидемиологических изысканиях.

3) Агентное моделирование, Agent-based model (ABM)^[13].

В известном смысле агентное моделирование – антипод системной динамики. ABM исследует динамику децентрализованных систем не по глобальным взаимосвязям, а на основании поведения ее индивидуальных «агентов», что называется «cнизу вверх».

«Агент — некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться»^[11].

Правила и законы на верхнем, глобальном уровне системы представляются функциями изменения состояния ее «нижних агентов».

Отцами ABM считаются математики Джон фон Нейман и Станислав Мартин Улам, внедрившие элементы агентного моделирования еще в конце 1940-х. Однако бум ABM начался в середине 1990- гг., когда вычислительные технологии достигли требуемых мощностей.

В числе многочисленных приложений, в которых агентное моделирование достигло значительных достижений, стал рынок ценных бумаг и управление инвестиционным портфелем. Успех ABM в трейдинге и инвестициях, во многом обязан синтезу с легендарным численным методом Монте Карло.

3.  ИЗ ИСТОРИИ МЕТОДА МОНТЕ КАРЛО

Рождение метода Монте Карло (ММК) относят к не очень уж и далекому 1949 году^[14]. Но отдельные «эксперименты», объединенные впоследствии под «брендом» ММК, проводились и гораздо раньше (см. ниже).

В 1949-ом появляется статья упоминавшегося выше Станислава Улама и Николаса Метрополиса с коротким и емким заголовком «Метод Монте Карло». В ней описывалась математическая методика имитационного моделирования, применявшая генератор случайных чисел (ГСЧ). Лучшим естественным ГСЧ была рулетка казино. Отсюда и название статьи, и название метода.

Почему именно «Монте Карло»? Свою роль сыграли родственные связи.

Дядя Н. Метрополиса был азартным игроком и много рассказывал племяннику об игорных заведениях княжества Гримальди. Круг предпочтений племянника был далек от увлечений греческого дяди. Его привлекали математика и физика. В 1937 г. Николас заканчивает Чикагский университет, в 1941-ом получает научную степень, а с 1943 г. работает у Роберта Оппенгеймера Лос-Аламосе над созданием атомной бомбы (Манхэттенский проект)^[15].

Н. К. Метрополис (1915-1999)[15]^[15]

Но о дядиных историях Метрополис не забыл, вспомнив имя святого, для «гонщиков за удачей» места, в совместной работе с Уламом.

Как ни печально это сознавать, но толчком ко многим научным открытиям середины XX века стало изобретение ядерного оружия, включая термоядерную бомбу. Не стали исключением и компьютерные технологии, численные методы и ММК. Одной из первых задач, в решении которой прорыв был обеспечен ММК, стало изучение движения нейтронов в изотропной (одинаковой по всем направлениям) среде.

4.  СУТЬ МЕТОДА МОНЕТ КАРЛО НА ПРИМЕРАХ ИЗ ЗАНИМАТЕЛЬНОЙ МАТЕМАТИКИ

Метод Монте Карло заключается в многократном повторении изучаемого процесса посредством генератора случайных чисел (величин), ГСЧ. Массив полученных исходных данных о системе служит источником ее вероятностных характеристик.

Простейшим образцом служит расчет среднего расстояния между двумя точками в круге. С помощью ГСЧ (величин) каждый раз определяется пара случайных точек в пределах данного круга и измеряется интервал между ними. Полученные оценки усредняют. Безусловно, чем больше количество измерений, тем более точным будет результат. Общее место для ММК и любого иного имитационного метода.

Ниже приведены два доступных математических примера применения метода Монте Карло.

4.1.  Французский граф, капитан и число π

В 1777 г. французским математиком, графом де Бюффоном была предложена оригинальная концепция вычисления числа π опытным путем.

Плоскость расчерчивалась параллельными прямыми, расположенными на расстоянии R друг от друга. На нее сотни раз бросалась игла длиной L. Взяв нехитрый двойной интеграл (опустим эту процедуру), граф получил следующую формулу для определения числа π:

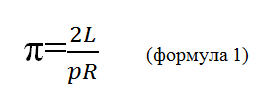
Здесь, p – отношение числа бросков, при которых происходит пересечение иглы, хотя бы одной прямой (число пересечений), к общему числу бросков. Ошибка уменьшается при увеличении общего числа бросков. На практике, для удовлетворительного результата оно должно исчисляться сотнями.

Как развлечь (и отвлечь) пытливый ум, когда тело выздоравливает?

Некий капитан Фокс в 1864 году не знал, куда себя деть, когда он восстанавливался после ранения. Скука смертная. Как-то он наткнулся на метод Бюффона, а может быть, капитан был еще и математиком-любителем и самостоятельно вывел формулу 1. Кто знает… Глаза Фокса загорелись. Это то, что нужно. То, что его отвлечет, развлечет и позволит с пользой провести время.

И капитан начал бросать иглу.

Итоги трех попыток Фокса сведены в следующую таблицу^[14]:

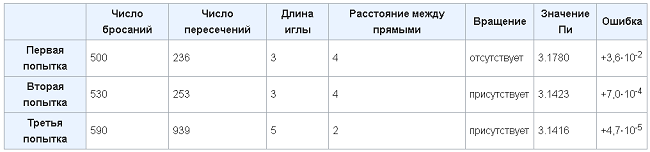
В попытке № 3 длина иглы L больше расстояния между прямыми R, что позволило увеличить точность эксперимента без существенного увеличения общего количества бросков иглы. Резко выросло число пересечений, так как игла за один бросок могла пересечь прямые несколько раз. В идеале, до трех раз. Вращение плоскости во второй и третьей попытках выздоравливающий капитан использовал для уменьшения системной ошибки.

Забавно, что длительный выход из физического недомогания и вызванная этим хандра, не единожды подтолкнули вперед активистов метода Монте Карло. Тот же Станислав Улам вплотную заинтересовался им, когда раскладывал пасьянсы приходя в себя после болезни. «Маленькие серые клеточки»^[16] мозга математика требовали интеллектуальной пищи, и Улам задался вопросом: «Какова вероятность того, что пасьянс сложится?»

С. М. Улам (1909-1984), фото с бэйджа лаборатории Лос-Аламоса^[17]

Можно было бы пойти по пути формул комбинаторики, но Улам применил теорию вероятностей и, повторив «карточный» опыт много раз, подсчитал вероятность выпадения удачных вариантов пасьянса.

Перефразированная цитата от Альберта Эйнштейна гласит: «Бог не играет в кости»^[18]. Но может быть, метод Монте Карло заставляет-таки его это проделывать?

4.2.  Вычисление определенного интеграла

Школьники старших классов и студенты первого курса университета или ВТУЗа при знакомстве с основами математического анализа учатся брать интегралы. Вначале неопределенные, потом определенные, затем кому повезет (или не повезет, это очень субъективно) более сложные типы: двойные, тройные, криволинейные интегралы и пр.

Взять определенный интеграл от функции f(x) на пределах от a до b:

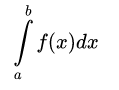
можно двумя способами.

1) Найти первообразную функцию Ф(x), такую, что ее производная Ф′(x)=f(x) и воспользоваться формулой Ньютона-Лейбница:

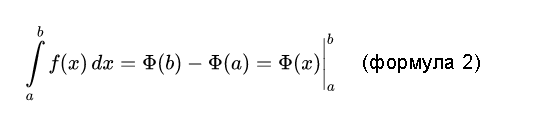
Просто и красиво. Как и все у Исаака Ньютона и Готфрида Лейбница. Но проблема в том, что вне курса матанализа поиск конечных и точных первообразных Ф(x) для «реальных» f(x), часто не имеющих строгой аналитической записи, почти безнадежное дело. А интегралы, будь они неладны, брать надо.

2) Тут на помощь приходит геометрия и геометрическая интерпретация определенного интеграла.

Строится график функции f(x) и высчитывается площадь криволинейной области (криволинейной трапеции), ограниченной линией графика и осью Х от a до b:

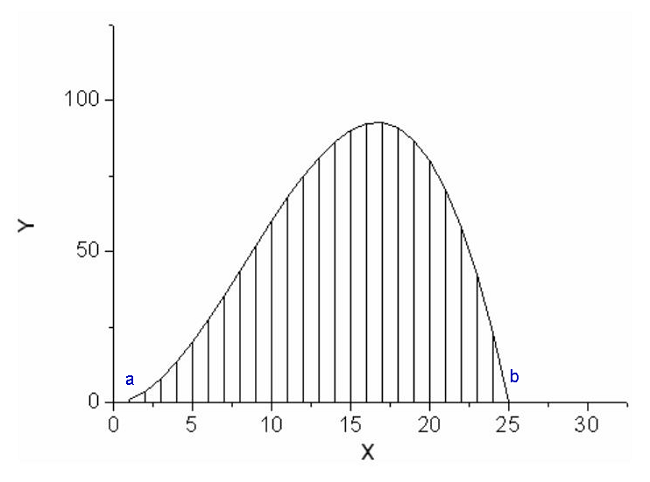
источник^[14]

Как высчитывается?

Фигура разбивается на n столбиков (прямоугольников) с номерами от 0 до n-1 (можно и от 1 до n), основание (ширина) которых равна ∆х_i, а высота (длина) примерно равна f(ξ_i), где ξ_i – значение аргумента x в i-ом интервале. Площадь этих столбиков суммируем, обязательно устремляя ∆х_i→0. Если разбиение происходит на неодинаковые отрезки, то к нулю должна стремится самая большая ширина: ∆х_max→0.

Строгий предел (lim) выводит на искомый определенный интеграл:

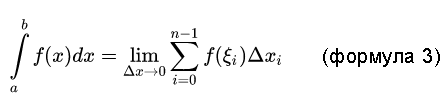
Если график уходит в отрицательную область оси Y, то берутся модули |f(ξ_i)| или все, в конечном счете, регулируется умножением на (-1).

Метод Монте-Карло дает возможность расчета определенного интеграла несколько с другой, вероятностной (случайной) точки зрения.

Вместо равномерного разбиения отрезка [a;b], на N подотрезков (обычно одинаковой длины), ММК «набрасывает» на [a;b] N случайных точек, и получает набор аргументов u_i:от u₁ до u_N. Для каждого из них определяется значение функции f(u_i) и производится следующая оценка определенного интеграла:

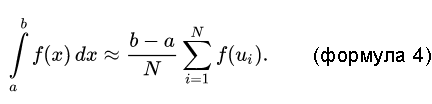
Казалось бы велика разница между формулами 3 и 4! В обеих, находи значения функции внутри выбранного интервала интегрирования, формируй суммы и получай результат.

Ан нет!

Концепция разная и, в конечном счете, трудозатраты тоже.

Для точности формулы 3 надо увеличивать и увеличивать количество подотрезков, выводя, в идеале, в область бесконечно малых значений их максимальные длины. В формуле 4 такой путь тоже приемлем, но по нему не надо идти столь уж фанатично. Дополнительно минимизировать погрешность возможно, набрасывая раз за разом, набор из одних и тех же N точек (их количество можно постепенно увеличивать) и усредняя полученные оценки определенного интеграла.

Более того, метод Монте Карло позволяет посчитать интеграл, вообще не трогая ось Х. Делается это следующим образом.

Приведем очередную картинку с графиком функции f(x):

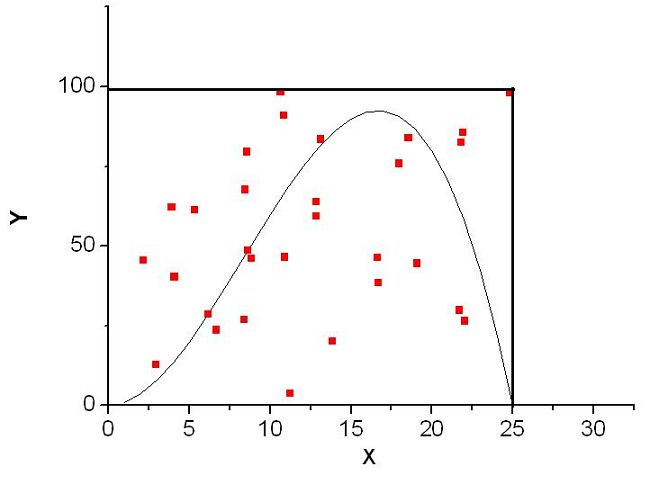
источник^[14]

Участник «ММК-эксперимента» отсекает область графика прямоугольником, параллелограммом или любой иной фигурой, важно, чтобы ее площадь S_par легко вычислялась. Далее, он бросает N точек уже не на ось ординат, а в выделенный прямоугольник. Подсчитывается число точек, попавших под кривую – K.

Оценка интеграла (площади S) выглядит так:

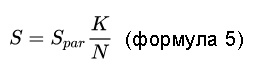
Опять же, для точности надо повышать N и делать оценку за оценкой (в том числе, и при одном и том же N) и усреднять результаты.

Таким образом, метод Монте Карло позволяет нестандартно решать знакомые задачи из школьного курса математики.

Но главное в ММК – как он помогает преодолевать сложные «взрослые» проблемы.

Владимир Наливайский

ПРИМЕЧАНИЯ И ССЫЛКИ 

(источник – Википедия/Wikipedia  или авторский комментарий, если не оговорено иное)

1. ↑ «Монте-Карло»
2. ↑ «Гримальди, Франческо»
3. ↑ «Монако
4. ↑ «Monte Carlo Casino»
5. ↑ «Marie Caroline Gibert de Lametz»
6. ↑ «Математическая модель»
7. ↑ «Трудно быть богом», повесть братьев Стругацких, 1964
8. ↑ Дихотомия – способ логического деления класса на подклассы, состоящий в том, что делимое понятие полностью делится на два взаимоисключающих понятия
9. ↑ «Линейная система»
10. ↑ «Нелинейная система»
11. ↑ «Имитационное моделирование»
12. ↑ «Дискретно-событийное моделирование»
13. ↑ «Агентное моделирование»
14. ↑ «Метод Монте Карло»
15. ↑ «Метрополис, Николас Константин»
16. ↑ Одно из любимых выражений Эркюля Пуаро, главного героя многочисленных романов Агаты Кристи
17. ↑ «Улам, Станислав»
18. ↑ «Альберт Эйнштейн», Викицитатник

ИСПОЛЬЗУЕМЫЕ СОКРАЩЕНИЯ

ММК – метод Монте Карло
ММ – математическая модель, коротко матмодель или модель. По тексту, обычно, то же самое, что динамическая система или коротко – система
ИМ – имитационное моделирование
ABM – Agent-based model, агентное моделирование, один из видов имитационного моделирования
ГСЧ – генератор случайных чисел (величин)
ВТУЗ – высшее техническое учебное заведение