В статье дано описание бета-коэффициента и бета-нейтрального (рыночно-нейтрального) инвестиционного портфеля. Продолжает цикл публикаций о приложении методов теории вероятности и математической статистики к операциям с ценными бумагами и другими финансовыми активами.
СОДЕРЖАНИЕ:
1. Бета-коэффициент ценной бумаги
2. Пример расчета Бета-коэффициента акции
3. Бета-коэффициент и риск портфеля ценных бумаг
4. Пример расчета Бета-коэффициента портфеля акций
5. Бета-нейтральный портфель и парный трейдинг
Примечания и ссылки
Используемые сокращения
1. БЕТА-КОЭФФИЦИЕНТ ЦЕННОЙ БУМАГИ
В конце прошлого века американский экономист, лауреат Нобелевской премии по экономике 1990 г. Уильям Форсайт Шарп (William Forsyth Sharpe) сделал допущение о линейной зависимости между среднерыночной доходностью (доходностью фондового индекса) и доходностью отдельно взятой ценной бумаги (ЦБ). Им была предложена следующая формула для расчета доходности ЦБ[1]:

Исходя из линейности связи между доходностью акции и индекса, У. Шарп предположил, что между этими случайными величинами имеет место полная корреляция, то есть, корреляционная зависимость с коэффициентом корреляции по модулю равным единице.

Уильям Ф. Шарп[2]
Таким образом, доходность отдельной ценной бумаги (акции) по формуле 1 содержит три слагаемых.
Первое, Альфа-коэффициент или коэффициент смещения, характеризует «собственный, несистематический» вклад по конкретной акции. Вторая компонента, равная произведению коэффициента, называемого Бета-коэффициентом или коэффициентом наклона, на доходность фондового индекса RI, отражает «систематическое, рыночное» влияние на доходность данной бумаги. Наконец, третий член правой части уравнения, ε, дает размер погрешности по i-ой акции, применение которого позволяет замкнуть в равенство первые два слагаемых слева и доходность акции справа.
Безусловно, формула 1 лучше работает для индексной бумаги. То есть для акции, входящей в корзину индекса RI. Тогда ri логично записать, как riI.
Интерпретировать спектр значений Бета-коэффициента (далее коротко по тексту «Бета») можно так:
- Бета<0 – обратная корреляция между доходностью акции и индекса, т.е. при увеличении RI, ri падает и наоборот.
- Бета=0 нет корреляции между акцией и выбранным индексом.
- 0<Бета<1 – прямая зависимость, волатильность (степень изменчивости) акции меньше волатильности индекса.
- Бета=1 – четкая прямая связь между акцией и индексом. Волатильности акции и индекса одинаковы.
- Бета>1 – прямая зависимость, положительная корреляция. Волатильность индекса выше волатильности данной акции.
Как ведет себя Бета при двух различных положительных значениях, хорошо иллюстрируются ниже приведенными рисунками[1] (ε принимается равным 0):
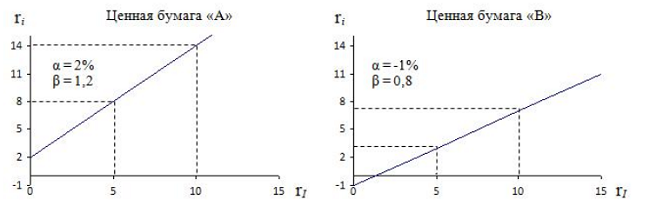
Для акции А: Бета=1,2 (>1), Альфа положителен и равен 2%. Для акции В: Бета=0,8 (<1), Альфа отрицателен и равен минус 1%. Из элементарной геометрии Бета – тангенс угла наклона прямой к оси абсцисс. Отсюда и второе название Бета – коэффициент наклона.
Больший угол наклона прямой для акции А к оси абсцисс (RI) обуславливает более резкое изменение ri при изменении RI, по сравнению с прямой для акции В. Кроме того, дан наглядный геометрический смысл Альфа-коэффициентов. Они дают значения ri при RI=0.
Бета рассчитывается следующим образом:

Что такое ковариация, дисперсия и среднеквадратичное отклонение (СКО) было подробно объяснено во вводной статье «Основы теории вероятностей для инвестора. От понятия вероятности до нормального распределения». Из формулы очевидно, что Бета не имеет размерности.
2. ПРИМЕР РАСЧЕТА БЕТА-КОЭФФИЦИЕНТА АКЦИИ
Определим Бета для акций Apple, на 22.03.19 крупнейшей в мире публичной компании по капитализации ($923 млрд)[3]. Главная торговая площадка – биржа NASDAQ. Тикер AAPL. Бумага входи в корзину ключевых американских индексов – DJIA (промышленный индекс Доу-Джонс) и S&P500.
В качестве временного периода выберем закончившийся 2018 год. Снимем[4] 15 значений цен закрытия AAPL за первое число каждого месяца с 01.12.17 по 01.02.19 включительно и соответствующие им значения S&P500.
Доходность (помесячную) акции и индекса (в %) посчитаем так:
(Sпосл-Sпред)/Sпред*100.
Здесь Sпред – предыдущее значение величины (цена акции или значение индекса), Sпосл – ее последующее значение.
Сведем полученные результаты в таблицу:
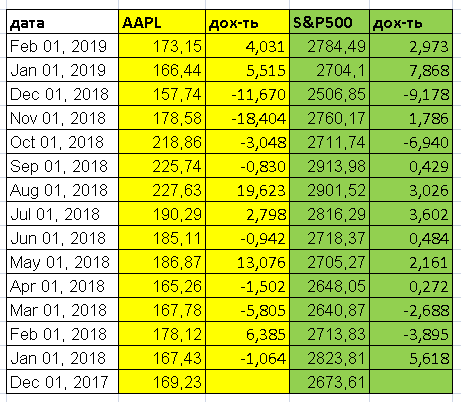
Желтый цвет отвечает акциям AAPL, зеленый – индексу S&P500.
Далее, в Excel применим к колонкам доходностей функцию КОВАР из раздела «Статистические». Получим значение ковариации cov(AAPL,S&P500)=16,344. Для вычисления дисперсии D(RI) можно использовать две формулы Excel из того же раздела статфункций: ДИСП и ДИСПР. Первая посчитает дисперсию для отдельной выборки, вторая – для генеральной совокупности значений. Что такое выборка и генеральная совокупность, и в чем их отличие, также смотрите в упомянутой выше статье нашего сайта «Основы теории вероятностей для инвестора…».
Делим ковариацию на дисперсии и получаем Бета, отдельно по выборке, Бета(выб.)=0,744 и по генеральной совокупности, Бета(гс)=0,802.

Получается, что акции AAPL (по генеральной совокупности) ведут себя по отношению к индексу S&P500 на рассматриваемом периоде, с выбранной (помесячной) частотой, почти, как акции В из примера предыдущего раздела (см. рисунок). Альфа-коэффициент не учитываем.
3. БЕТА-КОЭФФИЦИЕНТ И РИСК ПОРТФЕЛЯ ЦЕННЫХ БУМАГ
Формула для расчета Бета-коэффициента портфеля ценных бумаг (акций) имеет вид:

Бета связывает не только доходности бумаги и индекса (эталонного портфеля), но и риски отдельной ценной бумаги (ЦБ) и индекса. Напомним, что под риском ЦБ понимают дисперсию ее доходности (D) или СКО (σ)[5]: D=σ2.
В соответствии с «рыночной моделью» [1] полные риски бумаги и портфеля, в целом, записываются следующим образом:


Общий риск отдельной акции и всего портфеля зависит от рыночного риска (первое слагаемое βiI2σI2 для акции или βpI2σI2 для портфеля) и от собственного риска (второе слагаемое σεi2 для акции и σεp2 для портфеля).
Даже начинающий инвестор знает, что уменьшить суммарный риск по портфелю можно, проведя его максимальную диверсификацию. Увеличивая число акций различных компаний, трейдер смягчает негативное воздействие от неудач в отдельных позициях. Идеальным является случай, когда набор ЦБ полностью копирует индексную корзину, например, S&P500. Тогда β портфеля равно 1 (с учетом погрешности вычислений) и общий риск портфеля σp2 обусловлен только рыночным риском σI2.
Переход общего риска портфеля в рыночный риск, при увеличении числа представленных в нем компаний, демонстрирует график[1]:
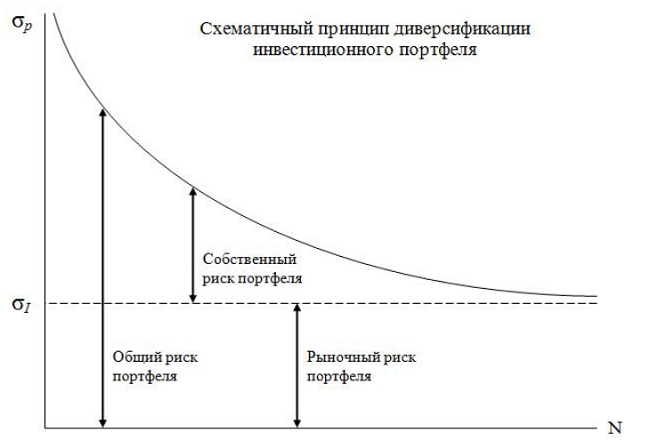
4. ПРИМЕР РАСЧЕТА БЕТА-КОЭФФИЦИЕНТА ПОРТФЕЛЯ АКЦИЙ
Согласно формуле 3, для расчета Бета портфеля надо знать Бета каждой акции (компании) и ее удельный вес в портфеле.
Допустим, необходимо определить на 01.02.2019 г. Бета портфеля, состоящего из рассмотренного выше Apple (AAPL), а также Microsoft (MSFT), Amazon (AMZN) и Facebook (FB). Эталоном вновь выбираем S&P500, временной период и частота съема информации, аналогичны примеру с Apple: котировки за первое число каждого месяца с 01.12.17 по 01.02.19.
Предположим, предпочтения инвестора по структуре портфеля таковы: 50% - AMZN, 25% - MSFT, 15% - AAPL и 10% - FB. Пусть, всего инвестировано $1 млн, тогда в AMZN вложено 0,5 млн, в MSFT – 0,25 млн, AAPL – 0,15 млн и в FB – 0,1 млн долларов.
Воспользуемся уже имеющимся массивом для AAPL и S&P500 и вытащим[4] соответствующие котировки для AMZN, MSFT и FB.
Обработаем котировки акций и значения S&P500, как это было сделано при расчете Бета для Apple выше. Сделаем допущение о том, что наши данные – генеральная совокупность помесячных значений исследуемых величин в интервале 01.12.17-01.02.19.
Сведем результаты в следующую таблицу:
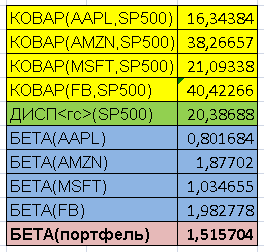
В желтом секторе таблицы высчитаны ковариации доходности акций относительно доходности S&P500. В зеленом поле –дисперсия доходностей S&P500 (уже рассчитывалась ранее). В голубом поле – Бета по каждой акции, равное отношению соответствующей ковариации к дисперсии доходности индекса. Наконец, в нижней строке таблицы итоговая Бета портфеля, исходя из весов каждой акции (компании).
Видно, что наиболее близко по доходности к индексу идет Microsoft (Бета=1,03), наиболее далек – Facebook (Бета=1,98). На прирост/падение доходности S&P500 на 1% акции компании Цукерберга реагируют на 2%.
Портфель с Бета=1,52 достаточно агрессивен – уровень риска на 52% выше среднерыночного по S&P500.
Как должен поступить инвестор, стремящийся снизить риск портфеля до среднерыночного (индексного), оперируя данными четырьмя эмитентами?
С одной стороны казалось бы, проще всего, наполнить весь портфель исключительно акциями MSFT с Бета=1,03. Но как же быть тогда с диверсификацией?
Исходя из Бета-коэффициентов, можно предложить увеличить удельный вес эмитентов в с Бета близкими к 1 и уменьшить вес бумаг, с Бета от 1 далекими. Например, структура портфеля с 50% MSFT, 30% AAPL, 15% AMZN и 5% FB даст общую Бета портфеля в 1,14. При этом, будет сохранена возможность неплохо заработать на резких движениях вверх AMZN и FB при росте доходности индекса.
Формируя портфель надо помнить и о дивидендах по акциям. В нашей модели, на анализируемом периоде, акционеров радовали Apple: три квартальные выплаты по $0,73 и одна $0,63 на акцию; и Microsoft: трижды по 42 цента и один раз по 46 центов на акцию.
Много это или мало? Суммарный дивиденд за рассматриваемый год по Apple – $2,82 на акцию, по Microsoft – $1,72 на акцию. Сравним с ценой акций на начало инвестирования (01.01.18) – Apple стоил $167,43, Microsoft – $95,01. Общий дивидендный поток за год составляет 2,82/167,43*100=1,68% на одну акцию Apple и 1,72/95,01*100=1,81% на одну акцию Microsoft. Здесь приблизительный паритет.
5. БЕТА-НЕЙТРАЛЬНЫЙ ПОРТФЕЛЬ И ПАРНЫЙ ТРЕЙДИНГ
Кроме единицы, другим ключевым значением Бета для портфеля является ноль. Портфель, для которого Бета=0, называется бета-нейтральным или рыночно-нейтральным. Нейтральность портфеля ценных бумаг или иных финансовых инструментов лежит в основе стратегии парного трейдинга.
Чем хорош портфель с Бета=1 или около 1?
Он исключает собственный риск. СКО доходности портфеля равно или почти равно СКО доходности фондового индекса. В смысле доходности, такой портфель движется вместе с индексом. Его доходность растет на росте доходности индекса, но, увы, падает при уменьшении доходности индекса.
Обнуление Бета приводит к тому, что доходность портфеля не реагирует на изменение доходности рынка и зависит только от соотношения между входящими в него акциями.
Как привести суммарный Бета портфеля к нулю?
Первый, наиболее понятный путь – ввести в него бумаги с положительными и отрицательными Бета. Рассчитав (подобрав) необходимые веса, можно свети Бета в ноль. Способ сколь понятный, столь и почти неосуществимый в реальной жизни. Найти акцию, которая бы устойчиво падала при росте индекса дело непростое. Да и насколько надежен подобный инструмент для длинных позиций?
Гораздо проще поступить иначе. Сформировать портфель из длинных и коротких позиций. Тогда для длинных позиций Бета будут традиционно положительными. Для коротких – отрицательными, по модулю равными положительным Бета, если бы такие бумаги приобретались.
Проиллюстрируем сказанное на примере котировок акций, приведенных в предыдущем разделе.
Если половину портфеля составить из короткой позиции по акциям Microsoft с Бета=1,035 (Бета больше), а вторую половину – из длинной позиции по акциям Apple с Бета=0,802 (Бета меньше), то итоговый Бета портфеля будет равен: -0,5*1,035+0,5*0,802=-0,116. Достаточно близко к нулю.
В наборе из двух акций очень просто вычислить веса так, чтобы Бета точно был нулевым. Достаточно решить систему двух уравнений с двумя неизвестными:

В нашем случае (Microsoft в шорт, Apple в лонг), решая систему, имеем X(Microsoft)=-0,4366, X(Apple)=+0,5634.
Проверка: -0,4366*1,035+0,5634*0,802=-0,0000342. То есть, с учетом округлений весов и Бет до тысячных – «крепкий» ноль.
На практике оперируют не одной бумагой против другой, а вводят коэффициенты, позволяющие корректно сравнивать рост/падение инструментов, приводя их цены к единой базе.
Как заработать на бета-нейтральном портфеле?
Подробно об этом написано в статьях категории «Парный трейдинг» нашего сайта. Необходимо выбрать пару акций или иных активов с высокой степенью корреляции (с коэффициентом корреляции близким к 1) и оперировать спредом. Открывать длинные позиции по недооцененной акции и короткие по переоцененной на широком спреде и закрывать их на узком спреде.
Особенно любят такие стратегии хедж-фонды.
В заключение необходимо отметить, что Бета-коэффициент отдельной бумаги или портфеля – величина непрерывно изменяющаяся и подлежит пересчету при переходе от одного таймфрейма к другому. Кроме того, она зависит от размера выборки котировок.
- ↑ «Бета-нейтральный портфель», Википедия
- ↑ «Шарп, Уильям», Википедия.
- ↑ https://finviz.com
- ↑ https://finance.yahoo.com
- ↑ «Cреднеквадратическое отклонение», Википедия
ЦБ – ценная бумага, по тексту под ЦБ понимается акция
СКО – среднеквадратичное (среднеквадратическое, стандартное) отклонение, σ
