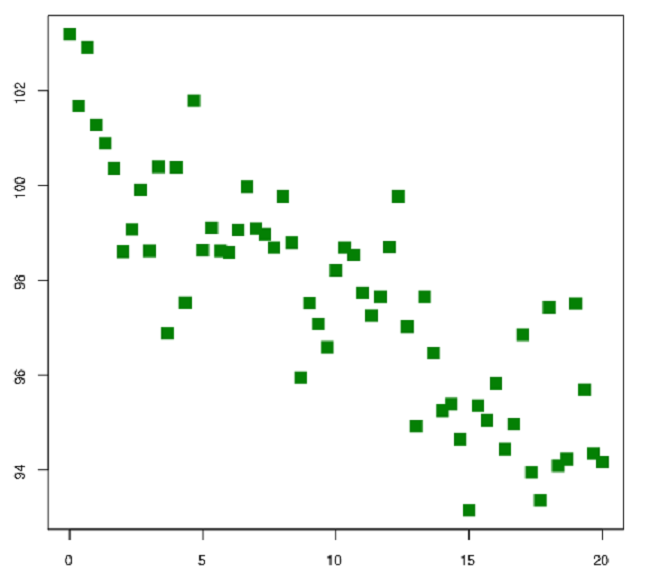
Материал продолжает тему теории вероятностей и математической статистики на финансовых рынках. Тема статьи – корреляция и ее использование в анализе поведения финансовых инструментов.
СОДЕРЖАНИЕ:
1. Понятие и примеры корреляции
2. Знак и степень корреляции
3. Ковариация и коэффициент корреляции Пирсона
4. Корреляция акций. Общие соображения
5. Корреляция акций. Примеры расчета
6. Корреляция на рынке forex. Практические аспекты
6.1. FX correlations table от Saxo Bank
6.2. Корреляционная таблица от OANDA
6.3. Сравнение коэффициентов корреляции от Saxo Bank и OANDA
Примечания и ссылки
Используемые сокращения
1. ПОНЯТИЕ И ПРИМЕРЫ КОРРЕЛЯЦИИ.
Корреляция в статистике[1] – «взаимосвязь двух или более случайных величин». Корреляционная зависимость заключается в том, что изменения значений одной или нескольких случайных величин приводит к «систематическим» изменениям другой или других величин (переменных).
У слова «корреляция» латинское происхождение: correlatio – взаимосвязь, соотношение.
В науке термин «корреляция» был введен в XVIII веке известным французским палеонтологом Жоржем Леопольдом де Кювье. Кювье применил разработанный им «Закон корреляции» в сравнительной анатомии для восстановления внешнего и внутреннего строения ископаемого животного по его отдельным останкам. Пионером корреляционного метода в статистике в конце XIX века стал англичанин Фрэнсис Гальтон.
Явление корреляции в матстатистике, имеет свои особенности. Она фиксирует только статистические взаимозависимости между величинами и выражает их количественную сторону, не более. Простой перенос, «калька» статрезультатов, их житейская интерпретация, вполне может навести на ложный след при установлении причинно-следственных связей.
В учебниках по статистике[2] приводятся забавные образцы корреляций, прямолинейная трактовка которых приводит к абсурдным выводам.
Так, безусловно, с точки зрения статистики, есть четкая корреляция между имущественным ущербом от пожаров в данном городе и числом пожарных, задействованных при их ликвидации. Чем выше ущерб и масштабнее огненное бедствие, тем больше пожарных занимаются его тушением. Однако обратный вывод: увеличение количества огнеборцев приводит к росту очагов возгорания – нонсенс. Еще большим «бредом» будет утверждение, что минимизировать последствия огненной стихии возможно уменьшением единиц пожарных расчетов.
Другой аспект заключается в том, что у корреляции двух и более величин может быть общая причина, формально лежащая за рамками выборки (массива данных). Например, можно выявить корреляционные связи между котировками акций нефтяных (и даже, в целом, энергетических) компаний различных стран, а также курсом российского рубля. Но повышение акций British Petroleum не обусловлено, в общем случае, ростом бумаг Exxon Mobil, а падение рубля – снижением бумаг «Роснефти». Центральным естественным источником подобных тенденций является цена галлона нефти и факторы, ее формирующие – увеличение/уменьшение нефтедобычи и пр.
Как любой иной феномен, корреляция доступна качественной и количественной оценке.
Для качественного описания полезно строить графики. В целях исследования корреляции двух случайных величин X и Y, достаточно стандартных осей координат на плоскости: горизонтальной оси x (оси абсцисс) и вертикальной оси y (оси ординат). По оси абсцисс откладываются значения X, по оси ординат – значения Y. Для финансового инструмента – его котировки.
Пусть рассматривается корреляция котировок двух ценных бумаг – акции А и акции В. X – цена акции А, Y – стоимость акции В. Получается двумерный массив точек с координатами (X;Y), котировками акций. Такая конструкция называется «диаграммой рассеяния» или «точечной диаграммой», по-английски scatter plot[4].
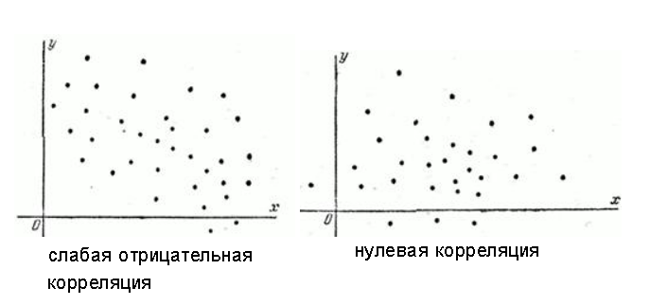
Примеры диаграмм рассеяния[3]
В целях количественной трактовки корреляции, теория вероятностей использует коэффициенты корреляции (подробнее см. ниже).
Если при возрастании одной случайной величины (переменной), в среднем[3] растет другая, относительно которой предполагается корреляционная взаимосвязь, говорят о положительной корреляции или прямой связи. Если при росте первой переменной, вторая, в среднем, убывает – имеет место отрицательная корреляция или обратная связь. У коэффициента положительной корреляции знак «+», у отрицательной – знак «–».
Вариант диаграммы рассеяния для положительной корреляции:
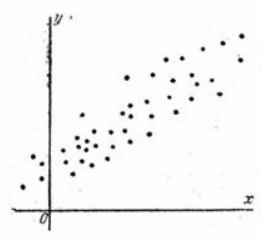
источник[3]
Хорошим примером отрицательной корреляции послужит картинка в преамбуле данной статьи и рисунок слева на двойной диаграмме рассеяния, приведенной выше.
Исходя из значений коэффициента корреляции или даже просто из визуального анализа диаграммы рассеяния, делают вывод о степени положительной или отрицательной корреляции. Могут отмечать сильную и слабую (высокую и низкую), а также максимальную и нулевую корреляцию (ее отсутствие). Образец нулевой корреляции – картинка справа на двойной диаграмме рассеяния.
Обычно, применяют коэффициенты корреляции по модулю не превосходящие 1. Поэтому максимальная положительная корреляция достигается на коэффициенте =+1, максимальная отрицательная на коэффициенте =-1. Если корреляции нет (случайные величины независимы), коэффициент корреляции=0. Все прочие случаи отвечают диапазону коэффициента корреляции (-1;+1).
Исчерпывающий, для понимания сути вопроса, набор диаграмм рассеяния представлен ниже:
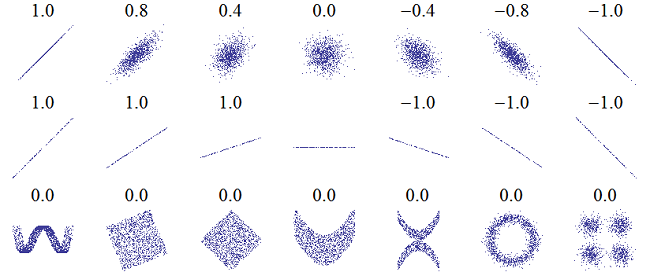
источник[1]
В верхней строке расположены варианты корреляций промежуточных степеней с коэффициентами корреляции 0,4 и 0,8 (положительная корреляция) и -0,4 и -0,8 (отрицательная корреляция). В центре строки корреляции нет (коэффициент=0), слева – максимальная положительная корреляция с коэффициентами +1, справа – максимальная отрицательная корреляций (-1).
Вторая строка отражает разные наклоны максимальных корреляционных зависимостей (прямых) с коэффициентами +\-1. В центре, по-прежнему, случай нулевой корреляции. Наконец, нижняя строка иллюстрирует корреляционные поля для независимых переменных с коэффициентом корреляции равным 0.
3. КОВАРИАЦИЯ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ПИРСОНА
Перед тем, как непосредственно перейти к формулам для коэффициентов корреляции, необходимо ознакомиться с таким понятием, как ковариация.
Ковариацией двух случайных величин X иY (другие названия: «корреляционный момент», «момент связи») именуется величина covXY, равная математическому ожиданию произведения отклонения случайных величин от своих матожиданий (средних):
covXY = M[(X-Xср)*(Y-Yср)] (формула 1)
Важные свойства ковариации:
1) Ковариация двух независимых величин равна 0.
2) Модуль ковариации двух случайных величин не превышает произведения их среднеквадратичных отклонений: |covXY| ≤ σXσY; или - σXσY ≤ covXY ≤ σXσY (*).
В принципе, уже covXY можно было бы использовать в качестве показателя корреляции величин X иY. Ковариация отражает, как взаимозависимость величин, так и их рассеивание (дисперсию). Но, как и в случае перехода от дисперсии к среднеквадратичному отклонению, когда надо было уйти от квадрата размерности, необходимо применить и некую модификацию covXY. Тем более, что в случае ковариации может быть не только квадрат размерности, но их произведение, когда анализируются величины, имеющие разные размерности. Кроме того, неплохо бы нормировать выстраиваемый коэффициент к единице, сделать его модуль не более 1.
Решение напрашивается, если приглядеться ко второму свойству ковариации. Разделив двойное неравенство (*) на положительную величину σXσY, получим:
-1 ≤ covXY/(σXσY) ≤ 1.
Отношение covXY/σXσY решает обе проблемы: оно безразмерно и по модулю не превышает 1. Именуется линейным коэффициентом корреляции или коэффициентом корреляции Пирсона, в честь английского математика-статистика Карла Пирсона. Принятое обозначение rXY.
Итак, коэффициент корреляции Пирсона rXY (далее по тексту, просто «коэффициент корреляции», «коэффициент» или кратко «КК») имеет вид:
rXY = covXY/(σXσY) (формула 2)
КК обладает двумя важнейшими свойствами.
1) |rXY| ≤ 1. Оно обсуждалось выше.
2) КК независимых величин равен нулю, что вполне естественно, так как согласно второму свойству ковариации, для независимых величин ковариация равна 0. Подобные величины называются также некоррелированными или несвязанными.
На деле, rXY рассчитывают, принимая в качестве матожиданий (средних значений) переменных X и Y их средние арифметические:
Xср = <X> = (1/n)∑xi
Yср = <Y> = (1/n)∑yi
где:
<X>, <Y> – средние арифметические значения случайных величин X и Y;
n – число измерений X и Y;
xi и yi – значения переменных X и Y на i-ом измерении;
индекс i – пробегает значения от 1 до n.
С учетом средних арифметических, для коэффициента корреляции rXY имеет место формула:
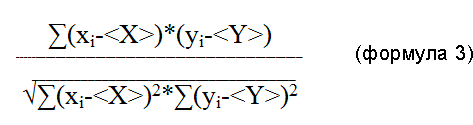
Для линейной зависимости между величинами:
Y = aX+b (формула 4)
коэффициент корреляции Пирсона равен +/-1. Случай корреляции максимальной степени. Знак КК совпадает со знаком коэффициента «a». Это вполне можно считать третьим важным свойством КК. При а=0 корреляции нет.
Чем ближе форма зависимости между X и Y к линейному виду, тем ближе КК по модулю к 1. Полностью коэффициент корреляции Пирсона упоминается иногда, как «линейный коэффициент корреляции Пирсона».
4. КОРРЕЛЯЦИЯ АКЦИЙ. ОБЩИЕ СООБРАЖЕНИЯ
Подытожим изложенную теоретическую часть для оценки корреляции финансовых активов. Начнем с ценных бумаг (акций).
Как уже отмечалось выше, случайными величинами X и Y служат котировки акций A и B. Исследуется набор из n пар котировок (X;Y) или n точек с координатами (X;Y) на диаграмме рассеяния. Каждая пара отвечает закрытию того или иного таймфрейма: от минутного до месячного или квартального. На средних сроках, как правило, анализируются цены закрытия торговой сессии (дня).
Коэффициент корреляции для разных временных периодов будет разным. То есть, если мы исследуем корреляции акций A и B на n=30 торговых днях в начале и в конце года, то получим разные результаты.
Целью изысканий является поиск пар акций с максимальной степенью корреляции (максимальным КК), положительной или отрицательной. В первом случае имеем прямую связь между величинами X и Y: с увеличением X, растет и Y; с уменьшением X, Y падает. Идеальная положительная корреляция – при коэффициенте rXY = +1.
Положительная корреляция помогает предсказать будущее движение одной акции в паре по уже наметившимся тенденциям по другой ценной бумаге.
Отрицательная корреляция соответствует обратной связи: при возрастании X, Y уменьшается, и наоборот. Для нее максимальный (по модулю) rXY = -1.
Отрицательная корреляция полезна при формировании бета-нейтральных (рыночно-нейтральных) портфелей. Теме бета-коэффициента и рыночной нейтральности будет посвящена отдельная статья сайта.
Если rXY для X и Y устойчиво не выходит далеко за пределы 0, то такие величины – некоррелированные или слабо коррелированные. Слово «далеко» может трактоваться по-разному. Примем для дальнейшего, что при |rXY| < 0,3 бумаги и иные финансовые инструменты будут считаться коррелирующими между собой в низкой (слабой) степени.
Математическим минимум корреляции любого знака будет ноль. При rXY = 0 корреляции нет, величины абсолютно независимы. Безусловно, в жизни, и максимальная (КК = +/-1), и нулевая (КК = 0) корреляции недостижимы.
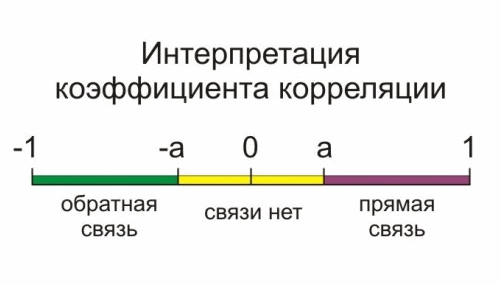
Те или иные приложения теханализа могут содержать сервис расчета коэффициента корреляции. По крайней мере, было бы разумным, чтобы он присутствовал. Онлайн-таблицы с КК для рынка forex представлены далее.
В любом случае, в Excel подобная возможность имеется. Функция «КОРРЕЛ» в категории «Статистические».
В «Массив1» вводим n котировок X, в «Массив2» - n котировок Y и получаем результат.
5. КОРРЕЛЯЦИЯ АКЦИЙ. ПРИМЕРЫ РАСЧЕТА
Для того, чтобы «почувствовать корреляцию вживую» проведем несколько расчетов КК для акций в Excel.
Исследуем, насколько взаимосвязаны тренды акций крупнейших представителей современных технологий – компаний Apple (AAPL) и Microsoft (MSFT).Первое и второе место в мировой капитализации публичных компаний на 18.03.19: $881 и $879 млрд[5] соответственно. Обе бумаги входят в корзины ведущих американских фондовых индексов DJIA (промышленный Доу-Джонс) и S&P500. Для обеих главная торговая площадка – биржа NASDAQ.
Периодом сравнения послужат два первых месяца текущего 2019 года. Источник информации – сайт[6]. Выбираем по тиккеру акцию, задаем требуемый период, частоту (дневные котировки) и вводим в массивы данных Excel цены закрытия бумаг.
Фрагмент таблицы «исторических цен» от Yahoo Finance для Apple:
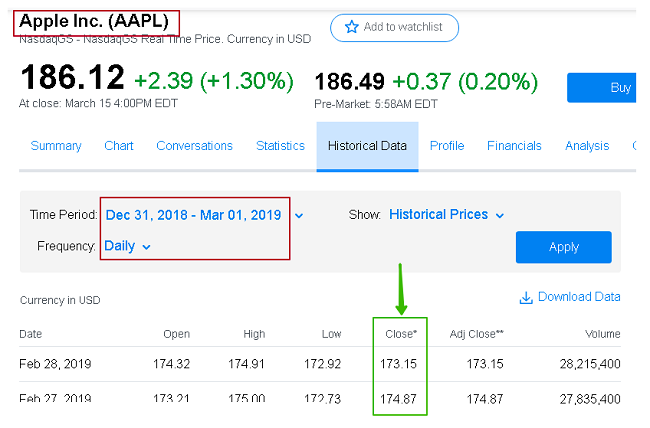
Всего 40 значений. Используем котировки со звездочкой (не учитывающие влияние дивидендной выплаты).
Проделав ту же процедуру для Microsoft и применив функцию «КОРРЕЛ» получаем коэффициент корреляции между акциями Apple и Microsoft:
rXY(AAPL-MSFT) = 0,7365.
Как указано выше, обе бумаги – в корзине S&P500. Интересно, насколько тесно они следуют за индексом, коррелируют с ним. Проделав описанный выше алгоритм, определим искомые коэффициенты корреляции:
между Apple и S&P500: rXY(AAPL-S&P500) = 0,9281;
между Microsoft и S&P500: rXY(MSFT-S&P500) = 0,8648.
Какие выводы можно сделать из результатов расчетов КК?
Акции Apple и Microsoft неплохо положительно коррелируют друг с другом с коэффициентом +0,7365. Обе бумаги демонстрируют прекрасную прямую зависимость с индексом S&P500, в который они включены. Лучший, в этом смысле, Apple (КК = 0,93, почти линейная зависимость), у Microsoft коэффициент чуть ниже – +0,86.
Такие показатели вполне предсказуемы. Обе акции – «очень» индексные и в силу мега-капитализации своих компаний сами формируют тенденции S&P500. В известном смысле, не они копируют индекс, а он «подражает» им.
Изложенное на словах наглядно иллюстрируется графиком сравнительной динамики инструментов[7]:
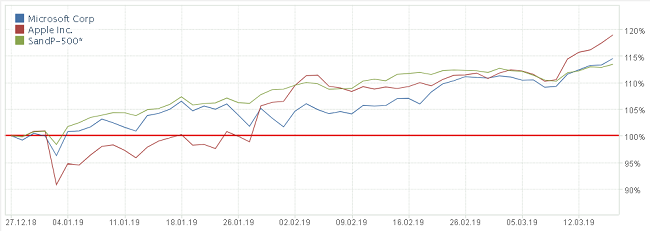
Изменение в % курса акций Apple, Microsoft и индекса S&P500. База расчета (100%) цены инструментов установлена на 27.12.18.
Отчетливо продемонстрирована хорошая положительная (прямая) корреляция Apple, Microsoft и S&P500. Вместе с тем, заметно, что Apple (красная кривая), в целом, идет ближе к индексу S&P500 (зеленая кривая), чем синий график Microsoft.
6. КОРРЕЛЯЦИЯ НА РЫНКЕ FOREX. ПРАКТИЧЕСКИЕ АСПЕКТЫ
С корреляцией на форексе дело обстоит несколько проще. Главное внимание трейдеров занимают всего один-два десятка ключевых валютных пар. Источникам финансовой информации не составляет большого труда генерировать актуальные данные требуемого объема.
В разделе представлены обзоры двух профильных интернет-ресурсов.
6.1. FX correlations table от Saxo Bank
Корреляционная форекс-таблица[8] от датского инвестбанка содержит коэффициенты корреляции на последнюю дату по девяти основным парам плюс золото/доллар.
Авторы приложения предлагаю корреляционные таблицы трех видов. В первой «Price versus price» приведены коэффициенты корреляций между валютными курсами. В двух других: «Price versus exposure» и «Exposure versus exposure» фигурируют показатели риска инструментов.
Временная шкала позволяет анализировать три периода. Первый – полный: с 17 ноября 2012 года по требуемую дату. Крайняя возможная дата анализа – текущая (или закрытый накануне торговый день). Второй и третий периоды короче – 90 и 30 дней до даты анализа.
Эту самую дату анализа или исследования можно изменять на более раннюю, перетягивая курсором специальный ползунок слева над таблицей. Он перемещается в интервале около года в прошедшее время от текущей даты. Таким образом, корреляционная таблица обновляется на интересующий день.
Для удобства восприятия, поля, в которых записаны коэффициенты корреляции для валютных пар (на пересечении строк и столбцов) закрашены в определенные цвета. Положительная корреляция (КК > 0) дана в сине-голубых оттенках, отрицательная (КК < 0) – в розово-красных.
При этом, чем коэффициенты корреляции выше, тем цвет насыщеннее. Например, набольшие положительные КК даны на темно-синем фоне, а самые крупные отрицательные КК – на бордовом.
Вот, как выглядит корреляционная таблица для валютных курсов от Saxo Bank на 20.03.2019. Период для вычисления коэффициентов корреляции – 90 дней до 20.03.19.
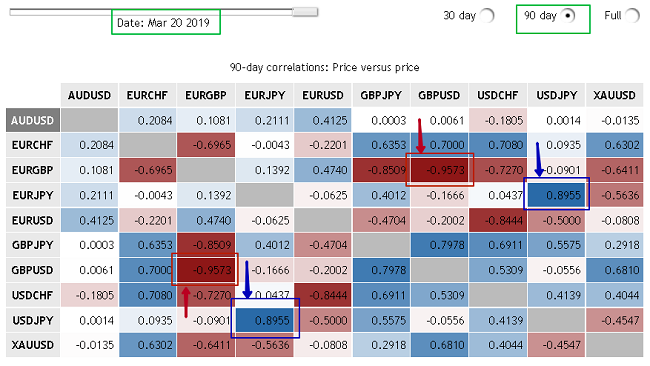
Даже беглый взгляд на табличную информацию позволяет сделать ряд выводов.
Максимум корреляции (КК = +0,8955) отмечен для пар [доллар/иена]-[евро/иена]. То есть, 90 дней (предшествующие 20.03.19) американский доллар и евро движутся максимально синхронно относительно японской иены. Темно-синие поля, синие рамки и стрелки.
Минимум (КК = -0,9573) наблюдается для пар [евро/фунт]-[фунт/доллар]. Почти линейная зависимость с отрицательным коэффициентом. Бордовые поля, красные рамки и стрелки. Безусловно, известную роль тут играет и то, что в первой паре фунт выступает котируемой валютой, а во второй – базовой.
Ниже таблицы Saxo Bank дает схематические графики изменения коэффициентов корреляции во времени. Можно посмотреть, как вел себя выше упомянутый КК для [евро/фунт]-[фунт/доллар] на выставленных 90 днях до даты расчета. Легко видеть, что таким радикально отрицательно большим он был далеко не всегда.
Вот картинка на 03.12.18:
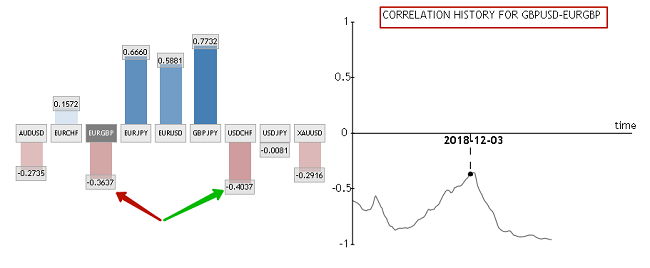
Коэффициент корреляции составлял всего минус 0,3637 (красная стрелка на диаграмме). Отрицательная корреляция была достаточно слабой. 3 декабря 18-го года отрицательно сильнее с парой фунт/доллар коррелировала пара доллар/франк, для нее КК = -0,4037.
6.2. Корреляционная таблица от OANDA
Второй рекомендуемый источник информации по коэффициентам корреляции – таблица от forex и CFD интернет-платформы OANDA[9].
Для корреляционного сравнения предлагается довольно широкая линейка инструментов:
- ключевые валютные пары: евро/доллар, евро/франк и пр.;
- прочие валюты в корреспонденции с ключевыми: гонконгский доллар, норвежская и шведская крона и пр.;
- металлы: золото, серебро, палладиум, платина в корреспонденции с рядом валют и между собой (золото/серебро);
- CFD (контракты на разницу) на ведущие мировые фондовые индексы, биткоин, нефть, медь, американские бонды и т.д.
Временная шкала тоже достаточно подробная. Периоды для вычисления коэффициентов корреляции: 1 час, 1 день, 1 неделя; 1, 3, 6 и 12 месяцев. Но расчет ведется только на текущее время (дату). Момент последнего обновления указан ниже таблицы.
Начало таблицы OANDA для главных валютных пар на 20.03.19 выглядит следующим образом:
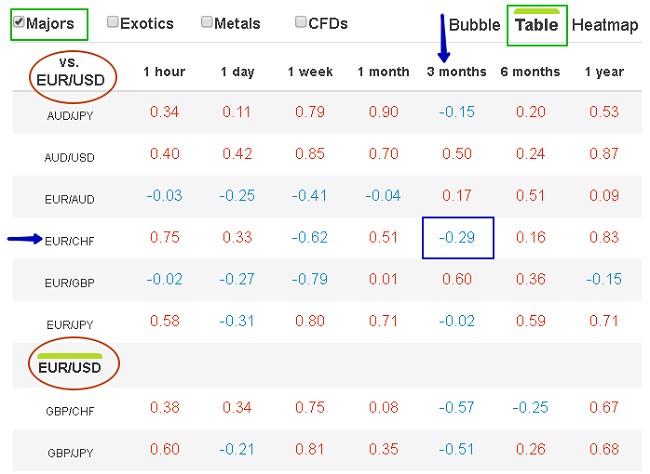
Читать данные надо так.
Сведения выводятся для основных форексных пар (поле Majors). Добавить или переключиться на другие инструменты можно через панель в верхней части таблицы. Поля Exotics, Metals и CFDs.
Базовый инструмент выбирается из левого столбца и после клика выводится в начало таблицы. В примере – это пара евро/доллар. Относительно нее и выдаются коэффициенты корреляции по прочим активам для каждого периода. Допустим, для пары [(евро/доллар-евро/франк] на 3 месяцах он равен минус 0,29 (синие рамка и стрелки).
Цветовую гамму авторы из OANDA выбрали ровно обратную, по отношению к таблице от Saxo Bank. Здесь голубой цвет – отрицательная корреляция (обратная связь), красный – положительная (прямая связь).
Таблица от OANDA доступна и без чисел. Опции «Babble» и «Heatmap» позволяют рисовать информацию в виде разноцветных пузырей или прямоугольных полей разных цветов, а в случае прямоугольников – и интенсивности. Такой сервис позволяет предварительно быстро находить требуемые знаки и степени корреляции и уже потом уходить в цифры.
OANDA предоставляет свою квалификацию силы корреляции:

6.3. Сравнение коэффициентов корреляции от Saxo Bank и OANDA
Безусловно, таблицы от OANDA более широки и информативны, чем сервис от Saxo Bank. Полезным будет сравнить представленные результаты. Понять, насколько они соотносятся между собой. Скорее всего, основа методик у обоих ресурсов одна и та же – формула 3. Но вот разбиение временных периодов на n точек могут отличаться.
Итак, сопоставим несколько КК, выложенные Saxo Bank и OANDA. Используем размещенные выше рисунки. Смотрим корреляцию девяти валютных пар относительно пары евро/доллар.
В таблице по 90 дням от Saxo Bank выделим строку евро/доллар. В таблице по евро/доллар от OANDA – столбец «3 months». Выведем в отдельную таблицу КК по девяти парам относительно пары евро/доллар (напомним, ситуация на 20.03.19):
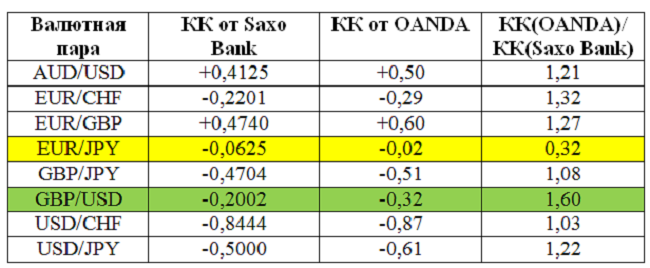
Отметим, в целом, сравнительно неплохое совпадение коэффициентов. По семи из девяти позиций КК отклоняются не более, чем на 32% друг от друга.
Исключений два.
Первое – пара [(евро/доллар)-(фунт-доллар)]. Зеленая строка. По ней КК от OANDA больше КК от Saxo Bank в 1,6 раза.
И уж совсем никак не соответствуют друг другу коэффициенты корреляции по паре [(евро/доллар)-(евро- иена)], выделено желтым. Единственный случай, когда КК от Saxo Bank превышает КК от OANDA. И как превышает, в 3,125 раза! Здесь явный разрыв.
Широкое применение корреляция находит при вычислении бета-коэффициента ценной бумаги и иного финансового инструмента и формировании бета-нейтрального (рыночно-нейтрального) инвестиционного портфеля. Это станет темой очередной публикации цикла.
- ↑ «Корреляция», Википедия.
- ↑ Елисеева И.И., Юзбашев М.М. «Общая теория статистики», Москва, издательство «Финансы и статистика», 2002. Приводится по источнику[1].
- ↑ Вентцель Е.С. «Теория вероятностей», Москва, издательство «Высшая школа», 1999.
- ↑ «Диаграмма рассеяния», Википедия.
- ↑ https://finviz.com
- ↑ https://finance.yahoo.com
- ↑ https://www.finam.ru/
- ↑ https://www.home.saxo/insights/tools/fx-correlations-table/tool-details
- ↑ https://www.oanda.com/lang/ru/
ИСПОЛЬЗУЕМЫЕ СОКРАЩЕНИЯ
КК – коэффициент корреляции (Пирсона), rXY