Трехфакторная модель Фама-Френча оценки доходности финансового инструмента (ценной бумаги), как продолжение однофакторной модели Capital Asset Pricing Model (CAPM). Учет риска капитализации компании и стоимостного риска ее ее акций. Основные подходы формирования инвестиционного портфеля, исходя из трехфакторной модели. Многофакторный подход в инвестировании.
Содержание:
- Введение. Коровьев-Фагот, бином Ньютона и “Факторная модель экспоненты”
- Начало. CAPM, как 1F-модель
- Появление 3F-модели Фама-Френча
- Премия за размер, SMBP (Small Minus Big Premium)
- Премия за стоимость. HMLP (High Minus Low Premium)
- 3F-модель. Немного практики
- Достижения и значение 3F-модели. Повышение факторности
- Что дальше? Все выше и выше
- Примечания и ссылки
- Используемые сокращения
Введение. Коровьев-Фагот, бином Ньютона и “Факторная модель” экспоненты
“Ну да, неизвестно,- послышался все тот же дрянной голос из кабинета,
- подумаешь, бином Ньютона!”
М. Булгаков “Мастер и Маргарита”
“Дрянной голос из кабинета” принадлежал Коровьеву-Фаготу, персонажу “Мастера и Маргариты” Михаила Булгакова, “гражданину престранного вида с глумливой физиономией”[1]. Общеизвестный факт.
Вряд ли далеко неглупый Коровьев считал бином Ньютона чем-то уж слишком мудреным. В нем нет ничего сложного. Изучается бином Ньютона еще в старших классах средней школы в курсе “Алгебра и основы математического анализа”[2].
Для тех, кто не в курсе, бином Ньютона - “формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных”[3]:
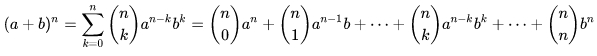
(формула 1)
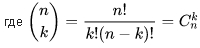
биноминальные коэффициенты, n - целое неотрицательное число, n!=1*2*3*...*(n-1)*n - (факториал числа n).
Cnk - число сочетаний из n по k.
Для частных случаев n=1, 2, 3 бином Ньютона приобретает привычный уже для школьника 5-6 класса вид:
(a+b)1=a+b. первая степень суммы;
(a+b)2=a2+2ab+b2, квадрат суммы;
(a+b)3=a3+3a2b+3ab2+b3, куб суммы.
Бином Ньютона - частный случай разложения функции (1+x)r в ряд Тейлора:
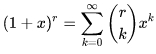
(формула 2)
В свою очередь, используя второй замечательный предел[4]:
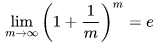
(формула 3)
где: e - число “e”, основание экспоненты и натурального логарифма, равное примерно 2,71828, можно вывести знаменитую формулу разложения экспоненты в степенной ряд:
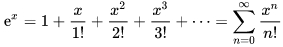
(формула 4)
При x=1 формула 4 позволяет вычислить число “е” с любой степенью точности, добавляя новые члены степенного ряда.
Результаты несложных вычислений сведем в следующую таблицу:
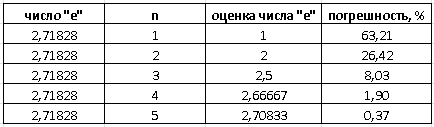
таблица 1
Здесь: n - число членов степенного ряда разложения экспоненты,
n=1, имеем ряд из одного члена - 1;
n=2, два члена 1+1/1!=2;
n=3, три члена 1+1/1!+1/2!=2,5 и т.д.
При оценке числа “е” ориентируемся на его “точное” значение с пятью знаками после запятой 2,71828. Видно, что уже при n=4 получаем достаточно приличное приближение с относительной ошибкой в 1,90%, а при n=5 погрешность падает и вовсе до 0,37%.
Введем понятие “Факторной модели” для оценки числа “е” или, в общем, для разложения экспоненциальной функции ex в степенной ряд с конечным числом членов (слагаемых).
Так, разложение вида:ex =1+x/1!=1+x, с двумя членами, содержащее х в первой степени (линейная зависимость), назовем “однофакторной моделью” для функции ex .
Соотношение ex=1+x/1!+х2/2!=1+x+x2/2, с тремя членами, с х в квадрате, назовем “двухфакторной моделью”, ex=1+x/1!+х2/2!+х3/3!=1+x+x2/2+x3/6, с четырьмя членами, содержащее х в кубе, назовем “трехфакторной моделью” экспоненты и т.д. В нашей таблице “факторность”=4, то есть имеем дело с четырехфакторной моделью оценки (в данном случае) числа “е”.
Очевидно, что, чем выше факторность модели, тем точнее получается выражение для приближения экспоненциальной функции, и, как следствие, числа “е”.
Перейдем от стройной, бесконечно красивой и предсказуемой математической вселенной к полному риска, угроз и подводных камней, миру реальных инвестиций и нервного трейдинга.
В материале, посвященном Альфе-критерию в инвестировании подробно изложена суть CAPM модели (Capital Asset Pricing Model) для оценки доходности бумаги/портфеля.
Напомним главную формулу CAPM с учетом Альфа-компоненты (α) :
E(Ri)=α+Rj+βi*(E(Rm)-Rj)
(формула 5)
где: E(Ri) - ожидаемая (рассчитываемая) доходность i-ой акции;
Rj - безрисковая ставка доходности, допустим доходность гособлигаций;
E(Rm) - доходность рыночного портфеля Rm, обычно доходность фондового индекса (S&P500, Доу-Джонс и др.), часто говорят - “бенчмарк”;
βi - Бета-коэффициент i-ой акции по рынку (индексу/бенчмарку) Rm.
Авторы концепции CAPM Уильм Шарп и Майкл Дженсен полагали, что доходность ценной бумаги определяется одним фактором - фактором рыночного риска, формализованным в премию за рыночный риск E(Rm)-Rj. В этом смысле, CAPM вполне имеет право именоваться однофакторной моделью (1F-моделью) оценки доходности финансового актива.
Разными авторами были предприняты попытки исследовать временную динамику премии за рыночный риск. Один из графиков[5] имеет вид:
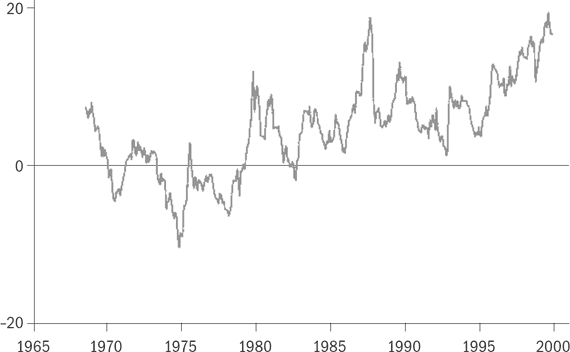
Премия за рыночный риск в годовом исчислении в 1965-2000 гг.
(график 1 по премиям)
Максимального значения в 20% за указанный период премия достигает дважды. Где-то между 1985 и 1990 годами, рядом с “черным понедельником” 19.10.1987, дня максимальной дневной волатильности индекса Доу-Джонса, потерявшего за одну сессию легендарные 22,61%. И ближе к краху доткомов 10 марта 2000 года. В 1970-1980 гг. премия находилась преимущественно в отрицательной области.
Если доходность некоей i-ой акции отличается от суммы безрисковой ставки Rj и произведения премии за риск на бету в большую сторону, то по мысли “отцов” 1F-модели имеет место положительная Альфа. Значит инвестиционный менеджер большой молодец, он обыграл рынок. В противном случае - победа за бенчмарком. Таким образом, подобные отклонения регулируются и объясняются всего лишь Альфа-критерием.
Теория была стройна, изящна и объясняла многое. За труды в области CAPM с формулировкой “За вклад в теорию формирования цены финансовых активов” У. Шарп (совместно с Г Марковицем и М. Миллером) в 1990 г. удостаивается премии по экономике имени Альфреда Нобеля[6].
Но, как впоследствии выяснилось, 1F-модель CAPM не дает толкование некоторым сравнительно тонким вещам в инвестиционной деятельности. Списывать частые удачи (большую положительную Альфу) отдельного (и довольно) большого класса инвесторов на божественный дар управления инвестпортфелем удавалось с трудом. И чем дальше - тем больше. Назрела насущная потребность повысить факторность модели оценки доходности финансовых активов.
Идея витала в воздухе.
Появление 3F-модели Фама-Френча
В 1993 году[7] (по другим источникам в 1992 г.) Юджин Фама, Eugene F. Fama и Кеннет Френч, Kenneth R. French вводят трехфакторную модель, названную по их именам: “Трехфакторная модель Фама-Френча”, далее по тексту используется сокращение “3F-модель Фама-Френча” или просто “3F-модель”.
Несколько слов о “действующих лицах”.

Юджин Фама (слева) и Кеннет Френч (справа)
Ю. Фама уже был подробно представлен на страницах нашего сайта, как экономист, оставивший существенный след в развитии гипотезы эффективного рынка (EMH). Прежде всего, как автор классификации форм рыночной эффективности (слабая, средняя и сильная). Представитель Чикагской экономической школы. Нобелевский лауреат 2013 года. Родился в 1939 г.
Кеннет Френч принадлежит к более молодому поколению ученых. Он на 15 лет моложе Фама (1954 г.р.). Работает в Tuck бизнес-школе Дартмутского колледжа, Ганновер, штат Нью-Гемпшир. Трехфакторная модель - пока его самое знаковое достижение.
В чем смысл новации от Фама и Френча?
Повышение факторности модели оценки финансовых активов. Скачок от одно- к трехфакторности. Говоря языком физики, переход от финансово-экономического одномерного “пространства”, в котором “объект” (доходность акции) перемещается по прямой, к трехмерному континууму, в котором он имеет три степени свободы.
Юджин Фама и Кеннет Френч расширяют базовую формулу CAPM для доходности акции, введя два новых члена:
E(Ri)=α+Rj+βi*(E(Rm)-Rj) +γ*SMBP+φ*HMLP
(формула 6)
где: SMBP (Small Minus Big Premium) - “премия за размер”, обусловленная риском превышения в портфеле компаний малой капитализации над компаниями большой капитализации;
HMLP (High Minus Low Premium) - “премия за стоимость”, возникающая от наличия в портфеле недооцененных акций;
γ, φ - коэффициенты линейной регрессии по SMBP и HMLP соответственно.
Формула 6 может быть интерпретирована, в том числе, и так. Доходность акции складывается из четырех видов доходности (премий): доходности безрискового инструмента, общей скорелированной Бетой доходности фондового рынка и доходностей, обусловленных риском владения акциями малых компаний и недооцененными акциями.
По-прежнему, первым слагаемым в формуле 6 от Фама-Френча, как и формуле 5 от Шарпа-Дженсена, идет Альфа-критерий (α). Но это разные Альфы. Большие α в формате Шарпа-Дженсена приписывают портфельным управляющим куда большее мастерство, чем у Фама-Френча. Из Альфы однофакторной модели Шарпа-Дженсена Фама и Френч вырезают большой кусок, введя два новых фактора.
Профдеятельность инвестора и трейдера связана с большим количеством разнообразных рисков. Они в них “купаются”. Каждую минуту. Чем (помимо прочего) и отличаются от математика и физика. За что и получают вознаграждения на порядки больше.
CAPM работает с одним видом риска - риском рынка, market risk. 3F-модель добавляет риск размера, size risk, и риск стоимости (недооценки), value risk. Пропущенная через спектр size-value картина становится более объемной и многогранной. Становится более реальной.
Тот, кто сознательно идет на дополнительные риски, отклоняя портфель от среднего положения, получает премии. Во всех смыслах. Инвестор не должен быть гением, уровня Леонардо в живописи, гоняясь за супер-Альфой в однофакторной CAPM-модели. Все гораздо “проще” - надо правильно учесть и корректно рассчитать дополнительные риски.
Премия за размер, SMBP (Small Minus Big Premium)
Двусмысленное изречение “Размер имеет значение” отлично работает на фондовом рынке, в смысле размера фирмы. Добавление в портфель акций компаний с низкой капитализацией повышает его волатильность и, при благоприятных условиях, может повысить его доходность.
Общая идея вычисления премии за размер, SMBP состоит из трех этапов.
- По определенной методике формируются две группы компаний - с наибольшей и наименьшей капитализацией на данной торговой площадке, в корзине данного индекса и т.д.
- За выбранный период рассчитывается усредненная доходность по каждой группе. Пусть доходность акций крупнейших компаний составляет R(cap_max), а бумаг их небольших визави - R(cap_min).
- Премия за размер выводится, как SMBP=R(cap_min)-R(cap_max).
Это крупными мазками, для ясности. Как всегда, возможно использование весов, усреднений, балансирующих и корректирующих коэффициентов и пр.
Источником информации для инвестора могут послужить профильные интернет-ресурсы. Например, базы данных сайта CRSP - Center for Research in Security Prices (Центр по изучению ценных бумаг). Наглядно увидеть масштаб разделения между крупными и малыми компаниями в режиме реального времени позволит Stock Screener от Finviz.
По уровню капитализации Finviz-скринер разбивает компании на шесть сегментов: от мега- до нано-компаний:
- Mega (мега) от $200 млрд.
- Large (крупные) $10-$200 млрд.
- Mid (средние) $2-$10 млрд.
- Small (небольшие) $0,3-$2 млрд.
- Micro (микро) $50-$300 млн.
- Nano (нано) до $50 млн.
Вот картинка по мега-компаниям на 25.12.2019.
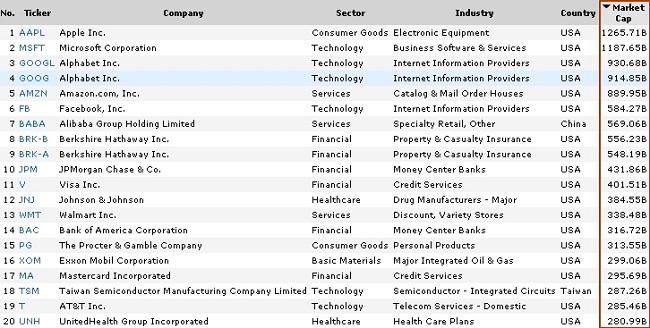
Первая двадцатка крупнейших по капитализации публичных компаний
Версия Finviz, 25.12.2019
Знакомые, у всех на слуху, мировые бренды. Лидеры - Apple, $1265 млрд и Microsoft, $1187 млрд. Прочие не дотягивают до триллиона долларов.
Самая маленькая у Finviz нано-компания на 25.12.2019 - Amira Nature Foods (ANFI) стоит “смешные” $0,8 млн.
Ниже приведен список двадцати публичных нано-компаний с наименьшей капитализацией. От меньшей - к большей.
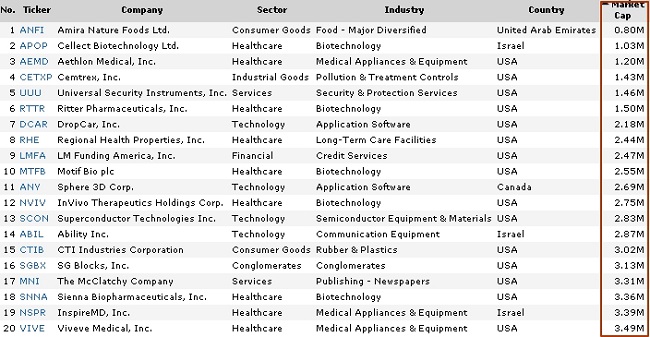
Первая двадцатка публичных компаний стоимостью до $50млн (по мере возрастания их капитализации)
Версия Finviz, 25.12.2019
25 декабря 2019 г. Apple Джобса и Кука стоит дороже арабских Amira Nature Foods в фантастические 1581250 (1,58 млн!) раз. Безусловно нет большого смысла комбинировать в одном портфеле такие позиции в ожидании супер-премии за размер SMBP. Тем более, что в данном конкретном случае, акции ANFI с апреля 2019 г. показывают отрицательную доходность, тогда как, бумаги AAPL неуклонно росли:
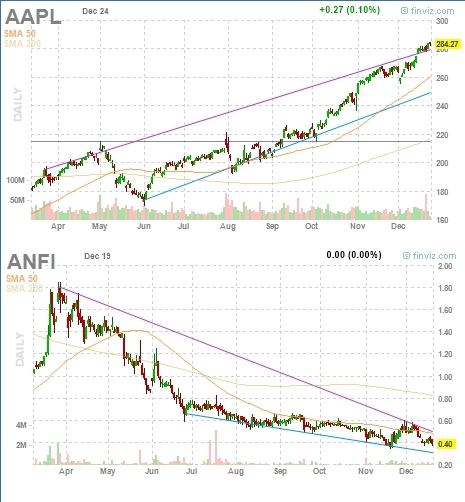
Более разумным представляется объединение не столь полярных категорий, а предположим, Large и Micro или Mid и Small. На практике часто используют медианный подход. Балансируют портфель из акций компаний, капитализация которых находится выше и ниже медианного уровня капитализации по выбранной бирже (индексу), допустим, по NYSE.
Цитируемый ранее источник[5] приводит следующую динамику премии за размер в последней трети прошлого века:
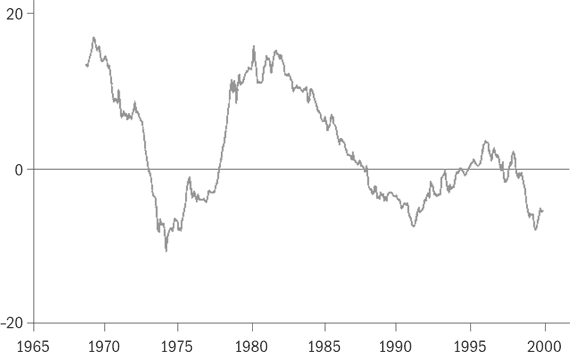
Премия за размер SMBP в годовом исчислении в 1965-2000 гг.
(График 2 по премиям)
Тенденции совсем иные, нежели в премии за рыночный риск (см. график 1 по премиям). Максимум SMBP, чуть ниже 20%, приходится на 1970-ый и 1980-ый годы, тогда как в 1980 г. премия за market была в районе нуля. И, напротив, в период бурного роста премии за рыночный риск в 1995-2000 гг., SMBP неуклонно снижалась от крайне небольших положительных уровней, глубоко заходя в отрицательную область.
Премия за стоимость. HMLP (High Minus Low Premium)
Рассмотрение стоимостных/недооцененных акций отсылает нас к истокам стоимостного анализа акций и стоимостного инвестирования, Value investing.
Главный вопрос вокруг которого крутится все стоимостное инвестирование - истинная, внутренняя, фундаментальная стоимость акции (intrinsic/fundamental value) и ее соотношение с текущей рыночной ценой. Если рынок идет ниже внутренней стоимости, акция считается недооцененной, ниже - переоцененной. В первом случае бумагу берут в лонг, во втором - в шорт. Положительную разницу между внутренней и биржевой ценой называют “запасом прочности” или “пределом безопасности”, Margin of Safety. Чем выше запас прочности по акции, тем выше потенциальная премия, HMLP по ней.
В теории все ясно, даже банально. Тривиальность резко заканчивается непосредственно перед отбором стоимостных акций. Единого рецепта не существует. Цитата от многолетнего последовательного сторонника Value investing “Волшебника из Омахи” Уоррена Баффетта: “Для вычисления истинной стоимости не существует никакой формулы. Вы просто должны хорошо знать тот бизнес, в котором собираетесь покупать пакет акций”[8].
Простейшим критерием стоимостной оценки акции признается отношение P/B, рыночной цены бумаги к ее балансовой стоимости. Можно сказать и так: отношение рыночной капитализации компании к ее чистым активам (собственному капиталу)[9].
(Другим стоимостным индикатором служит P/E - отношение рыночной цены акции к прибыли на одну акцию)
Традиционно принимают:
P/B<<1 существенно недооцененные акции;
P/B<1 недооцененные акции;
P/B>1 переоцененные акции;
P/B>>1 существенно переоцененные акции.
(Акции с P/B>1 и P/B>>1 называют растущими, growth акциями)
Finviz-скринер, отбирающий бумаги по фундаментальным показателям, классифицирует уровни P/B следующим образом:
P/B<1 - низкий (low);
P/B>5 - высокий (high).
Для более тонкой настройки по P/B введены десять категорий коэффициента класса Under (под, ниже): от Under 1 до Under 10; и класса Over (над, выше): от Over 1 до Over 10.
Задав low P/B<1 для нано-компаний, и отранжировав их по мере роста капитализации, получим такой список:
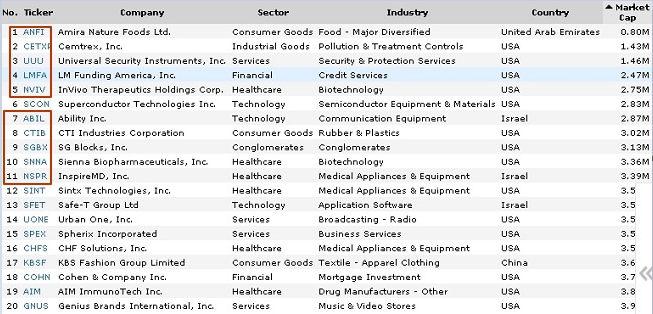
Первая двадцатка публичных компаний стоимостью до $50млн с P/B<1 (по мере возрастания их капитализации)
Версия Finviz, 25.12.2019
Нано-двадцатка с P/B<1 (двадцатка-2) заметно отличается от нано-двадцатки (двадцатки-1), не прошедшей через какой-либо фильтр, приведенной выше. Красными рамками выделены компании, попавшие в оба перечня. Очевидно, что за пределами двадцатки-2 остались ряд компаний начала и середины двадцатки-1 с капитализацией ниже $3 млн. По всей видимости, их P/B>1.
Согласно источнику[5], премия за стоимость (недооцененность) в 1965-2000 годах вела себя следующим образом:
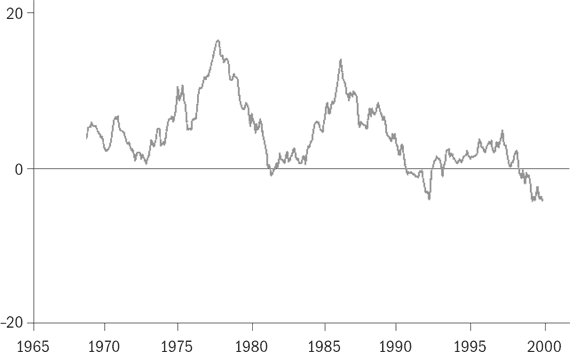
Премия за стоимость HMLP в годовом исчислении в 1965-2000 гг.
(График 3 по премиям)
Максимумы HMLP приходятся на 1977/78 и 1986/87 годы. Интересно, что в районе 1980/81 гг. HMLP топталась возле нулевой отметки, тогда, как премия за размер, SMBP была на пике. К 2000 году и HMLP, и SMBP дружно нырнули под ноль, а market risk премия рванула вверх.
Формирование портфеля на основе трехфакторной модели дает инвестору достаточно места для креатива и управленческой смекалки.
Общие этапы построения трехфакторного портфеля выглядят следующим образом.
1. За базу берется индекс. Проще говоря, инвестпортфель с той или иной степенью точности копирует выбранный индекс. Получаем индексный фонд. Это достигается различными путями. Если корзина индекса невелика, как у промышленного индекса Доу-Джонса с его 30 компаниями, не столь уж трудно самостоятельно приобрести все позиции, выдержав требуемый масштаб.
Для S&P500 задачка выглядит потруднее. Здесь на помощь придут ценные бумаги взаимных индексных фондов, заточенных под S&P500, например из линейки Vanguard 500; торгуемых на бирже фондов (ETF), самый известный - SPDR S&P 500 ETF Trust (тикер SPY), а также фьючерсы на индекс.
2. Индексный портфель разбавляется (отклоняется) акциями компаний малой капитализации и/или недооцененными бумагами. Методики ввода акций, генерирующих HMLP и SMBP, множественны и разнообразны. Именно здесь - точка приложения мастерства и профессионализма инвестиционного управляющего.
Для оценки премий SMBP и HMLP по выбранному рынку/отрасли/стране создаются и анализируются группы теоретических портфелей.
Один из вариантов процедуры выглядит так.
1. Отбираются акции высокой и низкой капитализации. Обычно, по медианному методу (см. выше). Результат - два инвестпортфеля. Назовем их ИП(cap_min) и ИП(cap_max).
2. Отбираются акции по коэффициенту P/B. Группируются три портфеля. В первый, ИП(P/B_min) войдут бумаги с минимальным P/B, P/B<<1, значительно недооцененные акции. Во второй, ИП(P/B_mid) - бумаги со средним P/B, допустим: 0,5<P/B<1,5. В третий, ИП(P/B_max), с высоким P/B, пусть с P/B>5, high-показатель по версии Finviz. Примем, что в ИП(P/B_min) - k штук акций, в ИП(P/B_mid) - m штук, в ИП(P/B_max) - v штук. Принятая пропорция: k/m/v=3/4/3. То есть, предположим, по 30, 40 и 30 позиций соответственно.
3. Далее, путем пересечения сформированных ИП, выделяют шесть новых портфелей:

таблица 2
В ИП(S/L) попадают акции недооцененные акции небольших компаний, в ИП(B/H) - переоцененные бумаги компаний с большой капитализацией и т.д. “⋂” - знак пересечения.
На практике, портфели можно формировать пропуская базовые ИП(cap_min) и ИП(cap_max) через фильтры по P/B. Скринеры акций, подобные Finviz, прекрасно реализуют подобную опцию.
Оценкой для премии за размер SMBP будут разности усредненных доходностей портфелей ИП(S/L), ИП(S/M) и ИП(S/H) с одной стороны и портфелей ИП(B/L), ИП(B/M) и ИП(B/H) с другой:
SMBP=1/3[R(ИП(S/L))+R(ИП(S/M))+R(ИП(S/H))]-
-1/3[R(ИП(B/L))+R(ИП(B/M))+R(ИП(B/H))]
(формула 7)
где: R(ИП(_/_) - доходности исходных инвестпортфелей.
В качестве ориентира премии за стоимость HMLP могут быть взяты разности средних доходностей портфелей ИП(S/L) и ИП(B/L) с одной стороны и ИП(S/H) и ИП(B/H) с другой:
HMLP=1\2[R(ИП(S/L))+R(ИП(B/L))]-1/2[R(ИП(S/H))+R(ИП(B/H))]
(формула 8)
Знаки у коэффициентов линейной регрессии γ, φ формулы 6 трехфакторной модели таковы.
γ при SMBP положительны для портфелей, с акциями малой капитализации, и наоборот, для портфелей с “дорогими” компаниями γ<0.
φ при HMLP положительны для портфелей, со стоимостными акциями (P/B<1), для портфелей с акциями, у которых P/B>1, φ<0.
Исторические данные по SMBP, HMLP и другим параметрам трехфакторной модели в различных секторах отдельных национальных экономик доступны на веб-странице Tuck бизнес-школы Дартмутского колледжа, постоянно обновляемой Кеннет Френчем.
Достижения и значение 3F-модели. Повышение факторности
Трехфакторная модель Фама-Френча неплохо зарекомендовала себя после появления в начале 1990-х. В целом, она объясняет уровни доходностей 90% диверсифицированных, отклоненных от центра (от индекса) инвестиционных портфелей. Показатель “старой” однофакторной CAPM - 70%[10].
Многочисленные выкладки показали, что на длинных горизонтах премии за размер и за стоимость, SMBP и HMLP, демонстрируют устойчивые, и (что важно) предсказуемые значения по данным корзине, сектору и стране. Для каждого рынка существуют свои “трехфакторные” наборы параметров. 3F-Инвестор осознанно получает значительные конкурентные преимущества.
Загадочная Альфа, занимающая в CAPM 30% доходности, сужается в 3F-модели до 10%. Значительный скачок, согласитесь.
Тем не менее, работы у инвестора, по-прежнему, немало. Ключевая задача - поиск оптимального соотношения между тремя факторами риска (премий) для формирования портфеля заданной доходности или, просто, для ее максимизации. Главное - обогнать индекс.
Трехфакторная модель получила не только лавры, но и критику. В частности, она не всегда давала удовлетворительные результаты для развивающихся рынков, emerging markets. Стоимостной фактор работает неплохо, а вот фактор размера (капитализации) проваливается. В 2013 году Foye, Mramor и Pahor высказали идею замены SMBP.
Но магистральным путем любого приближения, от экспоненты до доходности финансового актива, остается не замещение или модернизация уже привычных и доказавших свою работоспособность компонентов формулы доходности, а добавление новых. Другими словами, повышение факторности модели.
В 1997 году М. Кэрхарт, M.M. Carhart представляет на суд публике четырехфакторную модель (4F-модель).
Новация М. Кэрхарта состояла в ведении компоненты инерции, момента (модель именуется также моделью Моментума/Моментум-эффекта) WMLP - Winners Minus Losers Premium. Название емкое и хлесткое - премия по фактору “победители минус проигравшие”. Рассчитывается, как разница средней доходности акций компаний, показавших лучшую динамику за предыдущие 11 месяцев (победителей), и средней доходности бумаг с худшими показателями (лузеров).
Одна из формул для WMLP имеет следующий вид:
WMLP=1/2[R(Small_High)+R(Big_High)]-1/2[R(Small_Low)+R(Big_Low)]
(формула 9)
где: Small_High и Big_High - высокодоходные портфели акций компаний низкой и высокой капитализации соответственно.
Small_Low и Big_Low - низкодоходные портфели акций компаний низкой и высокой капитализации;
R - доходность портфеля.
Модель Кэрхарта можно дополнительно протестировать, оценивая, например, WMLP через высоко- и низкодоходные портфели, сгруппированные по стоимостному параметру (P/B) или по иным показателям.
Прогонка 4F-модели на разных рынках показала, что она весьма чувствительна к периодам наблюдений, что едва ли относится к ее сильным сторонам.
Наконец, совсем недавно, в 2015 г.[10] все те же Ю. Фама и К. Френч повышают ставки (читай, факторность) до пяти. Они вводят пятифакторную 5F-модель, включающую два новых слагаемых, два фактора в формуле оценки финансового актива (ценной бумаги).
Первый, RMWP - премия за рентабельность предприятия, представляющая разницу между доходностями компаний с высокой и низкой операционной рентабельностью. Второй, CMAP - премия за инвестиционную направленность (стратегию). В данном случае - разность доходностей фирм, ведущих агрессивную инвестполитику и компаний с консервативной инвестстратегией.
Исследования показали, что учет новых факторов 5F-модели делает излишним использование премии за стоимость HMLP, все покрывают другие четыре фактора: премия за риск, за размер, за рентабельность и за инвестполитику.
“Оставляя в горах, оставляя в горах своё сердце.
Я себе уже всё доказал:
Лучше гор могут быть только горы,
На которых ещё не бывал”.
В. Высоцкий “Прощание с горами”
Пятифакторная модель Фама-Френча в очередной раз сделала попытку уменьшения Альфа, объясняя доходность если не всех, то большинства портфелей через новые факторы риска (премии за риск).
Не получилось.
Сбой произошел на небольших фирмах, проводящих агрессивные инвестиции, при низкой рентабельности. Для выхода на реальные доходности их акций требовалось помощь в виде большой отрицательной Альфы.
И вот, уже за введение очередного, шестого фактора в 5F-модель выступает бывший студент-аспирант Ю Фама (PhD student) Клиффорд Скотт Эснесс, Clifford Scott Asness, основатель и руководитель хедж-фонда AQR Capital Managemen[11].
Эснесс не особенно оригинален. Он предлагает Моментум, фактор премии “чемпион-лузер”.
Итог - шестифакторная модель.
Позвольте сделать прогноз, итог промежуточный. Обнулить Альфу и здесь не удастся.
Будут (скорее всего, уже есть) новые эксперименты и, уверен, новые факторы №№ 7, 8 и т.д.
Кстати, каждый инвестор может “жонглировать” факторами самостоятельно, не дожидаясь подарков от экономических светил с Нобелевским статусом и без него.
Очевидно, что этим давно занимаются крупнейшие игроки.
Вот такой, понимаете “бином Ньютона”...
Владимир Наливайский
При подготовке статьи использованы материалы порталов Long/Short и Studme.
Примечания и ссылки (источник – Википедия/Wikipedia или авторский комментарий, если не оговорено иное).
- “Мастер и Маргарита”
- Точно было в школьной программе по математике в СССР, когда среднюю школу заканчивал автор данной статьи.
- “Бином Нютона”.
- “Замечательные пределы”.
- Бернстайн У. “Разумное распределение активов. Как построить портфель с максимальной доходностью и минимальным риском”.
- “Список лауреатов премии по экономике памяти Альфреда Нобеля”.
- Буренин А.Н. “Управление портфелем ценных бумаг”.
- “Уоррен Баффетт”, Викицитатник.
- В иностранной литературе широко используется также обратный коэффициент Book-To-Market (BTM). BTM=B/P=1/(P/B).
- “Fama–French three-factor model”.
- “AQR Capital Management”.
3F-модель (Фама-Френча) - трехфакторная модель Фама-Френча.
CAPM - Capital Asset Pricing Model, Модель ценообразования капитальных активов или Модель оценки финансовых <долгосрочных> активов, она же по тексту: 1F-модель CAPM.
4F-модель (Кэрхарта) - четырехфакторная модель М. Кэрхарта.
5F-модель (Фама-Френча) - пятифакторная модель Фама-Френча.
SMBP - Small Minus Big Premium, премия за размер в 3F-модели.
HMLP - High Minus Low Premium, премия за стоимость 3F-модели.
WMLP - Winners Minus Losers Premium, премия по фактору “победители минус проигравшие” в 4F-модели Кэрхарта (модели Моментума).
NYSE - New York Stock Exchange, Нью-Йоркская фондовая биржа.
ИП - инвестиционный портфель, инвестпортфель, коротко - портфель.
P/B - отношение рыночной цены к балансовой стоимости акции.
