Обзор модели ценообразования опционов Блэка-Шоулза. Используемые гипотезы, уравнение и формулы Блэка-Шоулза. Знакомство с коэффициентами чувствительности премии опциона к изменению входных параметров - “греками”. Материал подкреплен выдержками из профильных разделов математического анализа с наглядными примерами.

 

Содержание:

• Введение. Опцион
• Частные производные и дифференциальные уравнения

    Частные производные

    Частные производные высших порядков

    Дифференциальные уравнения

• Краткая история создания и авторы модели Блэка-Шоулза
• Гипотезы в основе OPM
• Уравнение Блэка-Шоулза
• Формулы Блэка-Шоулза

    Цена колл-опциона

    Цена пут-опциона

• Греки опционов

    Дельта (Δ)

    Гамма (Г)

    Вега

    Тета (Θ)

    Ро (ρ)

• Примечания
• Список источников
• Список представленных формул
• Используемые сокращения

 

Введение. Опцион

Опцион - один из самых интересных производных финансовых инструментов (ПФИ), и надо сказать, не из самых простых для понимания. 

Опционам посвящены три статьи сайта Rusforexclub:

• “Производные финансовые инструменты (деривативы). Введение (соответствующий раздел);
• “Опцион, основы. Московская Биржа”.
• ”Простейшие опционные стратегии”.

Освежим в памяти толкование опциона и его ключевых характеристик.

Опцион - срочный контракт, дающий его владельцу право на покупку или продажу базового актива по оговоренной цене на определенную дату (на протяжении определенного срока). 

Страйк (страйк-цена) опциона - цена исполнения опциона (покупки/продажи базового актива).

Премия опциона - его стоимость.

Колл-опцион, колл - опцион на покупку.

Пут-опцион, пут - опцион на продажу.

Американский опцион можно предъявить к исполнению в любой день до окончания периода его обращения.

Европейский опцион исполняется только на конкретную дату, указанную в контракте.

Между премией европейского опциона и стоимостью базового актива, а также его волатильностью, существует связь. Она отражена в модели Блэка-Шоулза.

 

Частные производные и дифференциальные уравнения

Перед тем, как начать знакомство с моделью Блэка-Шоулза полезным будет вспомнить несколько понятий из курса математического анализа.

Частные производные

Предполагая, что читатель помнит, что такое производная первого и более высокого порядков от функции одной переменной, остановимся на частных производных. 

Опуская строгое определение, использующее предел при исчислении бесконечно малых величин, воспользуемся практическим правилом взятия частной производной по функции с несколькими переменными. Рассмотрим функцию от трех переменных - f(x, y, z).

Для нахождения частной производной функции f по аргументу x, достаточно найти обыкновенную производную f по x, считая f функцией одного аргумента x. Другими словами, полагая, что при дифференцировании, переменные y и z выполняют роль констант. Аналогично - по другим аргументам.

Обозначается частная производная, как f’_x или ∂f/∂x.

Применим данное правило на конкретном примере.

Пример 1.

Пусть f(x, y, z)=2x²+y²-3z²-3xy-2xz.

Имеем:

∂f/∂x=4x-3y-2z

∂f/∂y=2y-3x

∂f/∂z=-6z-2x.

Частные производные - суть функции, в общем случае от тех же трех аргументов: x, y, z. В каждой конкретной точке трехмерного пространства найденные частные производные будут иметь числовые значения.

Допустим в точке (0;0;1):

∂f/∂x=4x-3y-2z=-2

∂f/∂y=2y-3x=0

∂f/∂z=-6z-2x.=-6.

Частные производные высших порядков

Производная от производной дает производную второго порядка, производная от производной второго порядка - производную третьего порядка и т.д. Принцип дифференцирования функции одной переменной распространяется (со своими особенностями) на взятие частных производных высших порядков по функции от нескольких аргументов,. 

Вот как выглядит полный набор частных производных второго порядка функции двух переменных z=f(x, y):

 

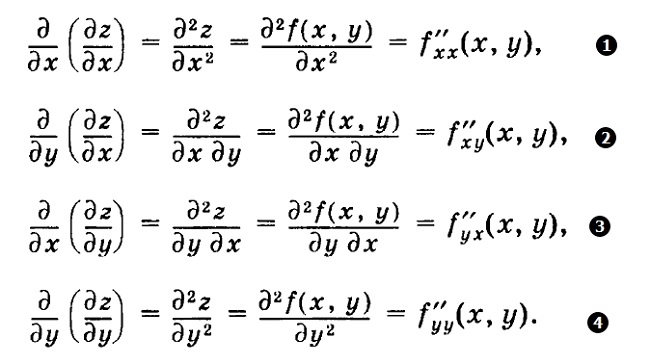
(формулы 1, М. Выгодский)

 

Вначале (1 и 2) берутся производные по x и y от ∂z/∂x. Далее (3 и 4) - производные по x и y от ∂z/∂y. Производные 1 и 4 называются “чистыми”, производные 2 и 3 - “смешанными”.

Дифференциальные уравнения

Дифференциальное уравнение - “Уравнение, содержащее производные неизвестной функции (или нескольких неизвестных функций)” (М. Выгодский).

Общий вид дифференциального уравнения (ДУ) n-го порядка с одной функцией одной переменной имеет следующий вид:

 

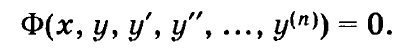
(формула 2, М. Выгодский)

 

Под порядком n ДУ понимается порядок (номер) наивысшей из производных, входящих в данное ДУ. 

Функция φ(x) является решением ДУ, если ДУ обращается в тождество при подстановке φ(x). Простейший случай решения ДУ - нахождение неопределенного интеграла, поэтому решение ДУ именуется также его интегралом, а процесс поиска всех решений - интегрированием ДУ.

Пример 2. Решение ДУ первого порядка.

Пусть требуется найти все решения ДУ первого порядка вида:

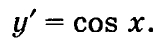
Решением такого уравнения есть неопределенный интеграл:

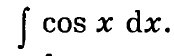
Следовательно, полный набор решений ДУ выглядит так:

y=sin x + C,

где C - константа.

В общем виде решение ДУ первого порядка содержит одну константу.

Пример 3. Решение ДУ второго порядка.

Теперь попытаемся найти все решения ДУ второго порядка вида:

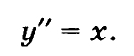
Перепишем его так:

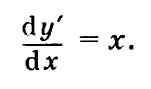
Умножив обе части на dx, и взяв неопределенный интеграл от обеих частей уравнения, получим:

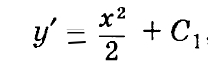
Еще раз проинтегрировав, выходим на полное решение ДУ второго порядка:

y=x³/6+C₁x+C₂

где C₁ и C₂ - константы.

В общем виде решение ДУ второго порядка содержит две константы.

Постоянные величины C из примера 2 и C₁, C₂ из примера 3 вычисляются под конкретные начальные условия - заданные значения x₀, y₀ и y’₀. 

Безусловно, приведенные случаи взятия производных и решения дифференциальных уравнений крайне примитивны и не преследуют иной цели, кроме, как помочь понять суть вопроса. На практике все существенно сложнее и подавляющее большинство ДУ даже первого порядка могут не иметь четкого аналитического вида.

В таком случае применяется широкий арсенал приблизительных вычислений. Многим методикам уже не одна сотня лет. Среди классических - приближенное интегрирование ДУ первого порядка по методу Эйлера и решение той же задачи путем разложения в ряд, предложенное Ньютоном. 

 

Краткая история создания и авторы модели Блэка-Шоулза

Главные принципы модели ценообразования опционов ее авторы Фишер Блэк и Майрон Шоулз представили в статье “Оценка опционов и коммерческих облигаций”, The Pricing of Options and Corporate Liabilities, вышедшей в журнале Политической экономики (экономии), Journal of Political Economy в номере 3 от 1973 г., том 81, стр. 637-654.

Как это часто водится в научной среде, модель получила название по имени своих создателей - модель Блэка-Шоулза. В дальнейшем, возможности модели были существенно расширены экономистом Робертом Мертоном. Именно Р. Мертон ввел термин “Модель ценообразования опционов Блэка-Шоулза”. 

В обобщенном варианте теория известна, как “модель Блэка-Шоулза-Мертона”. В англоязычной литературе применяется конструкция Black–Scholes Option Pricing Model, кратко - OPM. В дальнейшем, по тексту в качестве аббревиатуры модели Блэка-Шоулза будет использоваться данный англоязычный вариант - OPM.

Несколько слов об авторах OPM.

 

Слева направо - Ф. Блэк, М. Шоулз и Р. Мертон

(источники 4-6)

 

Фишер Блэк, Fischer Sheffey Black (1938-95).

Окончил Гарвард, с 1971 г. работал в Чикагском университете, далее - в школе менеджмента Массачусетского технологического института (МТИ). С 1984 года и до конца жизни - в Goldman Sachs. В 1994 году признается финансовым инженером года по версии International Association of Financial Engineers. В 2002 г. Американская ассоциация финансов,  American Finance Association учредила премию Фишера Блэка, которая каждые два года присуждается молодым экономистам.

Майрон Сэмюэл Шоулз, Myron Samuel Scholes (1941 г.р.).

Высшее образование получил в университете Мак-Мастера (Гамильтон, Канада) и Чикагском университете (степень PhD). Академическая карьера связана с МТИ, Чикагским и Стэнфордском университетами. В инвестиционном бизнесе отметился в Salomon Brothers. 

Роберт Кокс Мертон, Robert Cox Merton (1944 г.р.).

Учился в Колумбийском университете, Калифорнийском технологическом институте и МТИ, где в 1970 г. под руководством Пола Самуэльсона получил докторскую степень по экономике. Преподавал в МТИ и Гарварде. 

Помимо всего прочего, Шоулза и Мертона объединяют две вещи - Нобелевская премия и работа в хедж-фонде LTCM.

В 1997 году оба удостаиваются Нобелевской премии по экономике (премии по экономике памяти А. Нобеля) с формулировкой “За метод оценки производных финансовых инструментов”. Так международная научная экономическая общественность признала вклад лауреатов в развитие теории ценообразования опционов и прочих ПФИ.

Увы, в среду 10 декабря 1997 года Ф. Блэк не оказался рядом с коллегами в Стокгольмской ратуше в ожидании награды от шведского короля. К тому времени его уже не было в живых более двух лет, а посмертно, как известно, Нобеля не присуждают. Тем не менее, Нобелевский комитет упомянул его весомый вклад в разработку OPM. Это максимум, что может сделать комитет в отношении умершего потенциального кандидата в лауреаты. 

Теперь о хедж-фонде Long-Term Capital Management (LTCM). Ему посвящен отдельный материал на Rusforexclub. 

Шоулз и Мертон трудились в нем, как раз на момент получения Нобелевской премии. Фонд, как комета прочертил небосвод над Уолл-стрит. Четыре года (1994-98) его результаты поражали воображение торгующей публики. Рост чистых активов в семь раз, двузначные показатели годовой доходности, достигающие 40% годовых. Звездная команда управленцев, костяк которой составляли выходцы из легендарного Salomon Brothers. 

И среди стратегов - звезды мировой экономики М. Шоулз и Р. Мертон. 

К сожалению, в 1998 году все закончилось большим крахом. Азиатско-тихоокеанский кризис и технический дефолт в России подкосили LTCM. “Вечные двигатели” по производству прибыли фонда полностью разбалансировались и пошли вразснос. LTCM понес совокупные убытки в $4,6 млрд, в том числе, $1,6 млрд на свопах, $430 млн на инвестициях в российский и другие развивающиеся рынки и т.д. В сентябре 1998 года под контролем ФРС фонд проходит процедуру финансового оздоровления итогом которого стала смена владельцев LTCM, а в скором будущем - прекращение деятельности.

Творцы модели ценообразования опционов, ученые с мировым именем, ничем не смогли помочь. Скандал вокруг LTCM, связанный, в том числе, и в уклонении от уплаты налогов, выглядит не самой приятной страницей послужного списка авторов OPM.

 

Гипотезы в основе OPM

Любая (или почти любая) теория, будь-то математика, физика или экономика строится на неких допущениях, предположениях или постулатах. В математике принят термин “аксиома”. 

Речь идет об утверждениях, принимаемых без доказательств, которые используются для доказательств (построений) более сложных конструкций. В математике - теорем.

Например, физики в начале XX века ломали голову над объяснением движения электрона в атоме, не подчинявшееся классической ньютоновой механике. Окончательно противоречия сняла квантовая механика, но между ней и классической физикой была промежуточная, полуквантовая/полуклассическая планетарная боровская модель атома.

В ее фундаменте лежали два постулата Бора[1]:

1. Атом может находиться только в особенных стационарных или квантовых состояниях. Каждому такому состоянию отвечает определенный уровень энергии. Электрон не излучает электромагнитных волн при движении по стационарным орбитам.
2. При скачкообразном переходе между орбитами электрон (атом) излучает или поглощает кванты энергии.

Постулаты Бора, предложенные в 1913 году, позволили физикам перевести дух до создания квантовой механики в середине 1920-х годов. 

Модель Блэка-Шоулза не исключение. Она опирается на семь гипотез. Три относятся к активам (ценным бумагам, деривативам), торгующимся на рынке, четыре - собственно к рынку. 

Гипотезы по активам:

1. В течение срока действия опциона существует постоянная безрисковая процентная ставка, норма прибыли на безрисковый актив, допустим на гособлигацию.
2. Цены на финансовые инструменты изменяются на рынке согласно гипотезе случайного блуждания. Экономисты уточняют - в соответствии с моделью геометрического броуновского движения[2].
   
3. По акциям, являющимся базовым активом опциона, на протяжении срока его действия, дивиденды не выплачиваются.

Гипотезы по рынку:

1. Арбитраж (безрисковые сделки) невозможен.
2. Каждый покупатель ценных бумаг может взять кредит по безрисковой ставке для оплаты любого, сколь угодно малого пакета бумаг.
3. Трейдер вправе покупать и продавать любое количество (в том числе, дробное) ценных бумаг. Короткие продажи без покрытия проходят без ограничений. Продавец, открывающий short, немедленно получает деньги по текущей рыночной котировке.
4. Отсутствуют комиссии, сборы и иные транзакционные издержки при проведении сделок.

 

Уравнение Блэка-Шоулза

Математический фундамент модели Блэка-Шоулза - одноименное уравнение.

Уравнение Блэка-Шоулза связывает цену (премию) европейского опциона[3], как функцию двух переменных (стоимости базового актива и времени) с ценой базового актива, его волатильностью (среднеквадратичным отклонением) и действующей безрисковой ставкой доходности. Выводится уравнение, исходя из положений случайного блуждания (геометрического броуновского движения).

Дифференциальное уравнение Блэка-Шоулза в частных производных имеет вид:

 

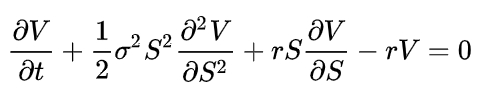
(формула 3, источник 3)

 

Здесь:

t - время от начала срока обращения опциона, в начале t=0, в конце t=T, где T - период обращения опциона;

S(t) - стоимость базового актива, как функция времени;

V(S,t) - цена (премия) опциона, как функция цены базового актива и времени;

σ - волатильность, среднеквадратичное отклонение (СКО) стоимости базового актива;

r - безрисковая ставка доходности.

Уравнение Блэка-Шоулза содержит четыре слагаемых.

Первое, ∂V/∂t - частная производная премии опциона по времени.

(В дальнейшем, прилагательное “частная” при слове “производная” может опускаться).

Второе, 

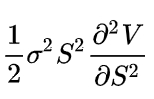
- производная второго порядка премии опциона по цене базового актива, умноженная на 1/2σ²S².

Третье, rS∂V/∂S - произведение производной премии по цене базового актива на саму величину базового актива S и безрисковую ставку r.

Наконец, четвертое слагаемое не содержит никаких производных. просто произведение безрисковой ставки на цену опциона, rV - безрисковый доход при вложении суммы V, в годовом исчислении.

Первые три члена входят в уравнение с одним знаком, при данной группировке слагаемых - со знаком плюс, четвертый - с противоположным знаком (минус).

 

Формулы Блэка-Шоулза

От уравнения Блэка-Шоулза перейдем к его важным следствиям, именуемым “формулами Блэка-Шоулза”. Они в явном виде представляют цены европейских опционов колл и пут. Говоря языком теории дифференциальных уравнений, находятся решения (интегралы) уравнения Блэка-Шоулза по функции V(S,t). 

Цена колл-опциона

Премия (цена)[4] опциона колл, выведенная из формулы Блэка-Шоулза, записывается следующим образом:

 

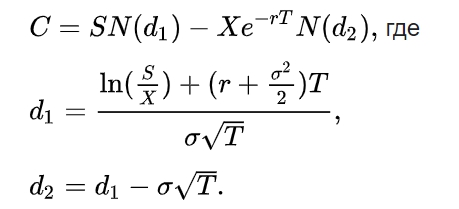
(формула 4, источник 2)

 

Что есть что в приведенном соотношении?

C - цена колл-опциона;

S - по-прежнему, стоимость базового актива, как функция времени, S=S(t);

r - безрисковая ставка доходности;

σ - волатильность, среднеквадратичное отклонение (СКО) стоимости базового актива;

T - время, оставшееся до исполнения (экспирации) опциона;

X - страйк-цена опциона;

N - интегральная функция распределения случайной величины, плотность вероятности которой задана нормальным распределением - стандартная нормальная функция распределения. 

Остановимся подробнее на стандартной нормальной функции распределения N.

Вначале, что такое (интегральная) функция распределения?

Функция распределения в теории вероятности - “Вероятность того, что случайная величина X примет значение, меньшее или равное х, где х - произвольное действительное число”. 

(Прилагательное “интегральная” часто опускается).

Записывается функция распределения F(x) так:

F(x)=P(X≤x)

(формула 5)

где P - вероятность события.

Стандартная нормальная функция распределения N(x) имеет вид:

 

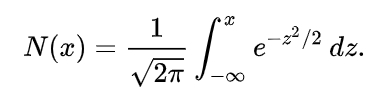
(формула 6, источник 3)

 

Ее производная N’(x) дает функцию плотности вероятность стандартной нормально распределенной величины или, кратко. стандартное нормальное распределение:

 

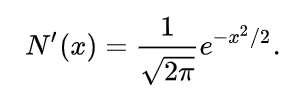
(формула 7, источники 3 и 15)

 

Аргументом x для функции N выступают сложные конструкции d₁ и d₂ (см. формулу 4), включающие натуральный логарифм от отношения стоимости базового актива к страйку, ln(S/X).

Цена пут-опциона

Цены (премия) P пут опциона по Блэку-Шоулзу:

 

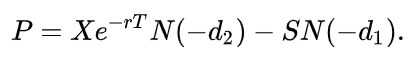
(формула 8, источник 2)

 

Обозначения те же, что и в формуле 4 для колл-опциона.

Беглый взгляд на формулы 8 и 4  обнаруживает зеркальную связь между ними. 

P=-C с заменой знаков аргументов функции N: d₁ на (-d₁), а d₂ на (-d₂). Подобная зависимость обусловлена симметрией между коллом и путом.

 

Греки опционов

Помимо расчета теоретических цен колл и пут-опционов, важнейшее значение для стратегии и тактики опционной торговли имеет вычисление специальных опционных коэффициентов, прозванных “греками”. Греки - так как используются буквы греческого алфавита.

Греки определяются непосредственно из формул Блэка-Шоулза путем взятия соответствующих частных производных от цен C и P колл и пут опционов. 

Греческие коэффициенты показывают, насколько чувствительны премии к изменению тех или иных величин. 

Ниже приведена таблица с пятью ключевыми греками: дельтой (Δ). гаммой (Г), вегой[5], тетой (Θ) и ро (ρ).

 

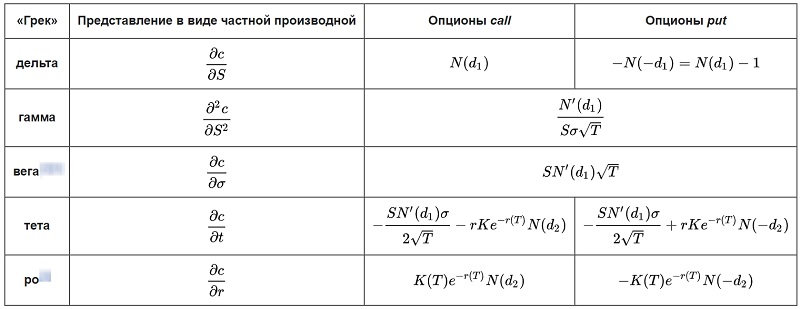
(здесь и далее в этом разделе формулы из источника 2)

 

Под “c” в таблице понимают стоимость V опциона (C для кола и P для пута), K - страйк-цена (X в формулах 4 и 8). Для теты и ро запись r(V) означает rV.

Разберем по порядку.

Дельта (Δ)

Самый известный грек. Первая производная премии опциона по стоимости базового актива, ∂c/∂S. 

Для колл-опциона:

∂C/∂S=N(d₁)

Для пута:

∂P/∂S=-N(-d₁)=N(d₁)-1

Дельта - скорость изменения премии опциона по цене базового актива. Чем она выше, тем более чувствительна премия данного опциона к изменению стоимости базового актива, чем ниже - тем менее восприимчива. При Δ=0 цена опциона никак не реагирует на движение цены базового актива. 

Согласно источнику 16, при Δ→1 велика вероятность исполнения опциона “в деньгах”, то есть владелец опциона получит прибыль при его экспирации (для колла - страйк будет ниже цены базового актива, для пута - выше). При Δ→0 ситуация меняется на противоположную, скорей всего при истечении срока действия опцион будет “вне денег”. 

Гамма (Г)

Вторая частная производная премии опциона по стоимости базового актива, ∂²c/∂S² или производная дельты по S: ∂Δ/∂S.

Для колл и пут опциона Г одинаковы и равны:

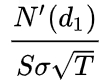
N’ - стандартное нормальное распределение, см. формулу 7.

Максимальных значений гамма достигает в точках резких изменений дельты. 

Используя дельту и гамму и применив разложение в ряд Тейлора до двух членов, можно вывести удобную формулу для приближенных, оценочных вычислений:

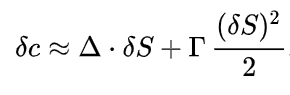
Изменение премии линейно связано с изменением цены базового актива через дельту и квадратично - через гамму.

Вега

Производная цены опциона по волатильности (СКО) базового актива, ∂c/∂σ - скорость изменения премии по волатильности базового актива.

Как и гамма, вега имеет одинаковое значение для коллов и путов:

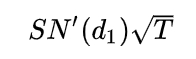
Вега всегда положительна, поскольку увеличение волатильности базового актива приводит к росту стоимости опциона. С приближением даты исполнения контракта вега снижается (источник 16). 

Вега - один из, так называемых, bastard греков. Смысл bastard греков заключается в том, что они выводятся путем дифференцирования премии по параметру, считавшемуся константой в формуле Блэка-Шоулза. В данном случае - по σ. Использование bastard греков чревато серьезными ошибками в опционном трейдинге.

Идентичность гамма и вега греков для колл и пут-опционов не случайна. Она обусловлена явлением, именуемым “паритетом пут-колл-опционов”, Put–call parity. Портфели, содержащие колл и пут-опцион на один и тот же актив эквивалентны. Если на момент экспирации цена базового актива выше страйка исполняется колл, в противном случае - пут. 

Тета (Θ)

Производная премии опциона по времени, ∂c/∂t - скорость изменения премии во времени. 

Здесь формулы посложнее.

Тета для колла имеет вид:

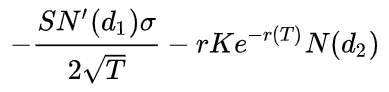
Для пута:

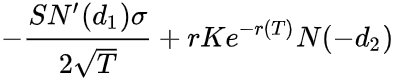
Первые слагаемые в соотношениях одинаковы, второе слагаемое у колла входит со знаком плюс, у пута - минус, и меняется знак аргумента у функции N: N(d₂)→N(-d₂). 

При неизменной стоимости базового актива цена опциона имеет тенденцию к снижению. Происходит “временной распад опциона”. Снижается “временная стоимость” опциона, зависящая от периода до погашения контракта[6].

Поведение теты можно истолковать так (источник 16). 

Максимальной по модулю тета становится накануне экспирации, когда опцион резко теряет в цене. В том случае, если тэта относительна невелика, то несмотря на временной распад, существует вероятность перепродажи контракта в зоне резких колебаний его цены. Кода тэта значительна, подобная возможность, скорей всего,  не представится.

Ро (ρ)

Заключительный в приведенном списке пятый грек, ро - производная премии опциона по величине безрисковой ставки r, ∂c/∂r. Наряду с вегой, еще один bastard грек. Формально дифференцирование происходит по константе r.

Ро для колла:

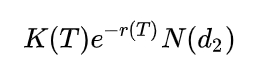
Ро для пута:

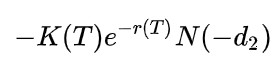
Как и ранее, налицо колл-пут симметрия. Ро для пута получается из ро для колла путем умножения на (-1) и замены знака аргумента у функции N.

Конечно, на практике никто вручную не считает теоретические премии, греки и прочие параметры опционов. Данные функции в онлайн-режиме выполняют приложения, поддерживающие торговый терминал трейдера опционами.

Ниже приведен скриншот фрагмента доски опционов с греками дельта и тета (источник 16):

 

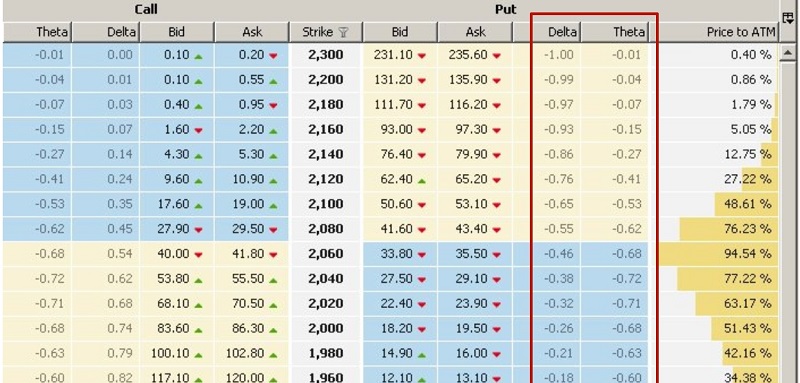
В заключении покажем, как выглядит уравнение Блэка-Шоулза, записанное с помощью разобранных греков:

Θ+1/2σ²S²Г+rSΔ-rV=0

(формула 9)

Лаконично и красиво.

 

Владимир Наливайский

 

На заставке - Hoplites fight Louvre, файл из Wikimedia Commons.

(гоплит - древнегреческий тяжеловооруженный пеший воин)

В подготовке статьи использованы материалы “Справочника по высшей математике” М. Я. Выгодского, Москва, АСТ, Астрель, 2006.

Первоисточниками определений терминов, понятий, явлений, вводимых по тексту, являются профильные статьи Википедии/Wikipedia, указанные в Списке источников к публикации, если не оговорено иное.

Примечания

1. Нильс Бор (1885-1962) - датский физик-теоретик, один из создателей современной физики, лауреат Нобелевской премии.
2. Геометрическое броуновское движение, GBM (экспоненциальное броуновское движение, экономическое броуновское движение) - случайный процесс с непрерывным временем, логарифм которого представляет собой броуновское движение.
3. В модели Блэка-Шоулза речь идет только о европейских опционах. В дальнейшем по тексту, под словом “опцион” понимается только европейский опцион.
4. Формулы Блэка-Шоулза дают теоретическую, расчетную цену опционов. 
5. Вега - не входит в греческий алфавит.
6. Текущая цена опциона формируется двумя составляющими: внутренней и временной стоимостью. Внутренняя стоимость определяется соотношением между страйком опциона и спотовой ценой базового актива. Если опцион “в деньгах”, его внутренняя стоимость положительна, в противном случае - равна нулю. Временная стоимость равна разнице между текущей рыночной ценой опциона и его внутренней стоимостью.

Список источников (Википедия/Wikipedia, если не оговорено иное)

1. “Гоплит”.
2. “Модель Блэка-Шоулза”.
3. “Black–Scholes model”.
4. “Блэк, Фишер”.
5. “Шоулз, Майрон”.
6. “Robert Cox Merton”.
7. “Journal of Political Economy”.
8. “Доктор философии”.
9. “Список лауреатов премии по экономике памяти Альфреда Нобеля”.
10. “Премия по экономике памяти Альфреда Нобеля”.
11. “Боровская модель атома”.
12. “Бор, Нильс”.
13. “Геометрическое броуновское движение”.
14. “Функция распределения”.
15. “Нормальное распределение”.
16. “Что такое греки опционов”, ihodl.
17. “Put–call parity”.

Список представленных формул

формулы 1 - частные производные второго порядка

формула 2 - дифференциальное уравнение n-го порядка с одной функцией одной переменной

формула 3 - уравнение Блэка-Шоулза

формула 4 - теоретическая цена колл-опциона

формула 5 - функция распределения

формула 6 - стандартная нормальная функция распределения

формула 7 - стандартное нормальное распределение

формула 8 - теоретическая цена пут-опциона

формула 9 - уравнение Блэка-Шоулза через греки

Используемые сокращения

LTCM - Long-Term Capital Management (хедж-фонд)

OPM - Black–Scholes Option Pricing Model, модель ценообразования опционов Блэка-Шоулза

PhD - Philosophiæ Doctor, доктор философии, аналог степени кандидата наук в России

ДУ - дифференциальное уравнение

МТИ - Массачусетский технологический институт

ПФИ - производный финансовый инструмент

СКО - среднеквадратичное отклонение