Ознакомительный материал о о генетических алгоритмах. Суть явления, виды, место в общем массиве торговых алгоритмов. Особое внимание уделено связи между естественными и искусственными генетическими процессами. Для широкого круга читателей.
СОДЕРЖАНИЕ:
ВВЕДЕНИЕ. Монах и горох
1. Генетика и естественный отбор, наследственность и изменчивость
1.1. Понятие генетики и естественного отбора
1.2. Генетическая информация. ДНК и хромосомы
1.3. Скрещивание, мутация и селекция
2. Генетический алгоритм. Определение и принцип действия
Этап 1. Начальная популяция и функция приспособленности
Этап 2. Размножение. Скрещивание и мутация
Этап 3. Селекция
Этап 4. Формирование нового поколения.
3. Пример. Генетический алгоритм и Диофантово уравнение
3.1. Диофантово уравнение и немного истории
3.2. Постановка задачи
3.3. Начальная популяция (родители)
3.4. Скрещивание, первые дети
3.5. Продолжение процесса и остановка
Примечания и ссылки
Используемые сокращения
Если путешествия во времени станут возможны, возникнет новая развлекательная индустрия. Назовем ее «Хронотуризм», а ее клиентов – «хронотуристами».
Представим хронотуриста, отправившегося на машине времени в Чехию 1860-х, точнее в город Брно (тогда Брюнне) в год, эдак, 1863-ий.
Что интересного можно было увидеть в провинциальном городке Австрийской империи, пусть и носившим гордый титул «столицы Моравии»?
Кто-то скажет: «Ничего, что там смотреть?» Конечно, если сравнивать Брно-1863 с античными Афинами, древним Римом и Египтом эпохи расцвета Фараонов, «кто-то» будет прав. Ратуша, несколько соборов, оперный театр… Готика, ренессанс и барокко. Кого этим удивишь. Вся старая Европа такая. С севера на юг и с запада на восток.
Проследим за нашим путешественником. Куда он пойдет? Быстрым шагом, нигде не останавливаясь, хронотурист минует «достопримечательности» чинного Брюнне и подходит к Августинскому аббатству Святого Томаша[1].
Устремляется к ограде, прижимается к ней лбом, костяшки пальцев, сжимающие кованые прутья, побелели от напряжения, дыхание учащается. Напряженный взгляд прикован к монастырскому саду.

Вид на монастырский сад Августинского аббатства Святого Томаша[1]
Что пытается разглядеть путешественник во времени? Заглянем из-за его спины.
Монастырский сад. В дальнем углу фигура в черном склонилась над кустом. Вроде, горох, если вы что-то понимаете в ботанике.
И всё.
Глаза хронотуриста расширились, в них запылало пламя. Такой взгляд у человека, одержимого наукой. Наш странник грезит биологией, точнее генетикой.
Перед ним – внешне ничем не примечательный монах Августинского аббатства Святого Томаша по имени Грегор.
Ученый-самоучка, автор прохладно принятых современниками «Опытов над растительными гибридами» 1866 г., послуживших основой Законов наследования моногенных признаков, впоследствии получивших его имя.
Отец классической генетики Грегор Иоганн Мендель разогнулся, поправил очки, подобрал рясу и перешел к следующему кусту.
Монах и горох, монастырь в Брно, далекий 1863 год…

Грегор Иоганн Мендель (1822-1884)[2]
1. ГЕНЕТИКА И ЕСТЕСТВЕННЫЙ ОТБОР, НАСЛЕДСТВЕННОСТЬ И ИЗМЕНЧИВОСТЬ
1.1. Понятие генетики и естественного отбора
Генетика – «наука о законах наследственности и изменчивости организмов»[3]. По объектам исследования различают генетику человека, животных, растений и микроорганизмов. По применяемым методам – молекулярную, экологическую, медицинскую, биохимическую генетику и т.д.
Генетика тесно связана с естественным отбором (эволюцией). По сути, это одно и то же природное явление, последовательные этапы которого описываются отдельными разделами биологической науки.
Под естественным отбором понимают магистральный эволюционный процесс, при котором количество особей с максимально благоприятными признаками (наиболее приспособленных, живучих) увеличивается, тогда как число особей с неблагоприятными или менее благоприятными признаками сокращается[4]. Достигается это через механизм генетического наследования.
1.2. Генетическая информация. ДНК и хромосомы
Каждая клетка живого организма содержит о нем закодированную информацию. Наследственный материал получил название «геном»[5]. Подавляющее большинство геномов, в том числе, геном человека, состоят из ДНК[6], у ряда вирусов геном формируется из РНК[7].
Генетическая информация генома комплектуется из генов. «Ген — единица передачи наследственной информации и участок ДНК, влияющий на определенную характеристику организма»[8]. Совокупность генов именуют генотипом[9].
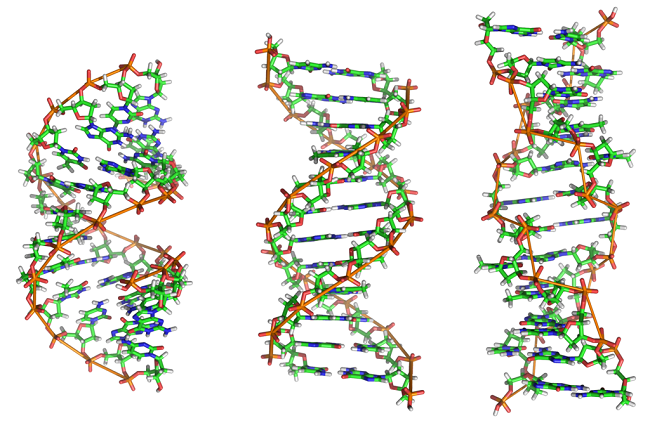
ДНК в разных формах[8]
С точки зрения химии, ДНК – длинная полимерная молекула в виде двойной спирали, состоящая из различных комбинаций четырех блоков, нуклеотидов. Каждому нуклеотиду присвоена латинская буква: A, G, T, C. За генетическую информацию отвечает порядок следования, чередования нуклеотидов в ДНК – генетический код. Генетические сведения, в конечном итоге, должны быть прочитаны и использованы клеткой при синтезе биополимеров, ее кирпичиков.
Каждая молекула ДНК окружена оболочкой – хромосомой и находится в ядре клетки. Для сохранения целостности генетической информации, хромосомы в ядре отделены друг от друга.
Человеческий геном состоит из 23 пар хромосом и одной отдельной ДНК[10]. В них зашито 28 тыс. генов.
1.3. Скрещивание, мутация и селекция
При размножении происходит слияние родительских половых клеток, их ДНК образуют ДНК потомства. Синтезируется дочерняя молекула ДНК. Процесс, названый репликацией ДНК[11], заключается в разделении родительских ДНК на две части, с их последующим обменом и сшиванием в новую, дочернюю ДНК. Исходя из перекрестного характера, он известен, как скрещивание, кроссовер или кроссинговер (cross-over, crossing over).
Репликацию можно рассматривать, как часть более общего биомеханизма: рекомбинации. Рекомбинация – «перераспределение генетического материала (ДНК или РНК) путем разрыва и соединения разных молекул, приводящее к появлению новых комбинаций генов или других нуклеотидных последовательностей»[12].
Таким образом, генетическая информация от родителей точно передается детям. Обеспечивается наследственность и изменчивость.
При нестандартных внешних условиях (радиация, окисление и пр.) ДНК способны мутировать (изменяться, повреждаться). Потомство будет наследовать иной, смещенный набор генов. Если мутация приводит к получению полезных свойств, они могут закрепиться и обеспечить скачок в развитии вида.
Процедура естественного отбора интенсифицируется и подправляется селекцией. Селекция пришла на смену простому искусственному отбору и позволяет «воздействовать на растения и животных с целью изменения их наследственных качеств в нужном для человека направлении»[13]. Мощный импульс современной селекции придала генная инженерия.
2. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ. ОПРЕДЕЛЕНИЕ И ПРИНЦИП ДЕЙСТВИЯ
Под генетическим алгоритмом (далее по тексту ГА) понимают «алгоритм решения задач по оптимизации и моделированию путем случайного подбора с привлечением механизмов естественной эволюции»[14]. В ГА встроены такие понятия классической генетики как, наследование, изменчивость, мутация и скрещивание.
Почином в области симуляции природного отбора стали исследования Нильса Баричелли, выполненные им в 1954 г. на компьютерах Принстонского института перспективных исследований. Отцом генетических алгоритмов считают американца Джона Генри Холланда, автора книги «Адаптация в естественных и искусственных системах», Adaptation in Natural and Artificial Systems (1975).

Дж. Г. Холланд (1929-2015)[15]
Упрощенно алгоритм создания и функционирования ГА выглядит так:
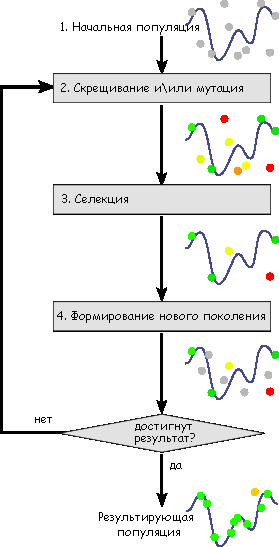
Схема работы генетического алгоритма[14]
ЭТАП 1. НАЧАЛЬНАЯ ПОПУЛЯЦИЯ И ФУНКЦИЯ ПРИСПОСОБЛЕННОСТИ
Создатель генетического алгоритма, «беря на себя функцию» природы или, высказываясь с пафосом, Создателя, формирует стартовую группу виртуальных, искусственных особей. Группа заточена под решение, оптимизацию выбранной задачи. Каждая особь – некий вектор, строка или, говоря генетически, генотип, хромосома или ДНК, включающая определенный комплект формализованных элементов. Ими могут быть число, единица информации (бит), иной объект. Аналог гена в традиционной генетике.
Например, для уравнения, решение которого аналитически не всегда выполнимо, подобным вектором (хромосомой) станет набор из его приблизительных корней, подстановка которых даст возможность решить уравнение с той или иной степенью точности. Для инвестиционного проекта генотипом выступит вариант или стратегия инвестирования, содержащий строку из нескольких бюджетов (расходов на проект) или иных элементов, выполняющих роль генов.
К сожалению, в «генно-алгоритмической» литературе присутствует известная путаница в использовании приведенных терминов. Так, иногда геном называют хромосому, что не совсем корректно и с точки зрения биогенетики, и пр. Надо быть внимательным и ориентироваться по ходу изложения.
Отобранные особи оцениваются, как хорошо они решают поставленную задачу, насколько «жизнеспособны». Делается это через функцию приспособленности (ФП), fitness function.
Функция приспособленности — «вещественная или целочисленная функция одной или нескольких переменных, подлежащая оптимизации в результате работы генетического алгоритма, направляет эволюцию в сторону оптимального решения»[16].
ФП проверяет представителей нулевого и следующих поколений. Исходя из приведенных выше сценариев для ГА, в качестве ФП могут выступать погрешность в решении уравнения или критерий успеха инвестпроекта (чистая начальная стоимость, внутренняя норма доходности, срок окупаемости, рентабельность).
Особенно стараться при выборе кандидатов в стартовую популяцию не стоит – в процессе работы алгоритм все подправит. Главные требования – соответствие требуемому формату данных, способность размножаться и возможность корректного расчета ФП.
ЭТАП 2. РАЗМНОЖЕНИЕ. СКРЕЩИВАНИЕ И МУТАЦИЯ
После тестирования начальной популяции посредством ФП, для размножения отбираются особи с лучшими параметрами выживаемости и жизнеспособности. Они подвергаются процедуре скрещивания (кроссовера): искусственные родительские ДНК (хромосомы) разрываются и обмениваются фрагментами. Цель – улучшить потомство. При необходимости, используется внешнее вмешательство в генотип – мутация.
Преимущественное направление выбора родителей – случайная сортировка, результат работы генератора случайных чисел.
Для того, чтобы и здесь была некая система, применяют три пути формирования пары:
1) Панмиксия – «папа» и «мама» подбираются случайно.
2) Инбридинг – «папа» (первый родитель) выбирается случайно, а «маму» (второго родителя) ищут максимально похожую на «папу».
3) Аутбридинг – «папа», по-прежнему, случаен, но предпочтение отдают той «маме», которая меньше всех напоминает «сильную половину».
Все очень подобно человеческим судьбам, вы не находите?
Основной посыл – «сильное», «здоровое», если хотите, «красивое» потомство, в свою очередь, способное при скрещивании произвести «хороших и симпатичных» детей.
Согласно установленным критериям, функция приспособленности отбирает лучших из «родившегося» потомства. Они формируют очередное новое поколение, готовое к размножению. Прочим – «дорога на кладбище».
У селекции в генетическом алгоритме есть одна тонкость. Несмотря, на фазы отбора, размножаться должно максимальное число участников. Идеально – все. На практике, после каждой стадии сильные должны тянуть с собой какую-то колонию слабых и скрещиваться не только в парах сильный-сильный, но и в дуэтах сильный-слабый. Здесь особенно эффективны и востребованы мутации.
В противном случае, по меткому выражению автора одной из статей о ГА[17], уже сразу, на двух-трех первых циклах, создатель генетического алгоритма получит «альфа-самца», супермена (или супервумен), который/которая подомнет под себя всю популяцию, «взгромоздится на трон», окружит себя копиями-подражателями, и о дальнейшем плавном улучшении детей речь уже не пойдет.
Простейший принцип отбора – «турнирная селекция». После кроссовера случайным образом выбираются пары особей. Победитель в паре. тот у кого значение ФП лучше. Среди других подходов можно отметить вероятностные методы рулетки, ранжирования, равномерного ранжирования и сигма-отсечения[14].
ЭТАП 4. ФОРМИРОВАНИЕ НОВОГО ПОКОЛЕНИЯ.
Логическое завершение третьего этапа.
Далее, племя генотипов гоняется генетическим алгоритмом по этапам 2-4. И так – до остановки.
Остановка имеет место в трех случаях.
1) Результат достигнут и решение найдено.
2) Количество поколений, предусмотренных ГА на эволюцию, исчерпано.
3) Закончилось время отбора.
3. ПРИМЕР. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ И ДИОФАНТОВО УРАВНЕНИЕ
Суть алгоритмической генетики будет проиллюстрирована на линейном Диофантовом уравнении (ДУ).
Использование генетического алгоритма для поиска корней линейного ДУ – излюбленное рунетовское объяснение смысла ГА для новичков (смотрите, в частности[17]). Не претендуя на оригинальность, покажем и мы, как работает ГА для этой задачи. Образец привлекает доступностью и наглядностью, и красив математически, что немаловажно.
3.1. Диофантово уравнение и немного истории
Прежде всего, что такое Диофантово уравнение?
ДУ – уравнение вида: P(x1,…, xn)=0
Где P – целочисленная функция, обычно полином с целыми коэффициентами, переменные xi также принимают целые значения[18]. Названо по имени древнегреческого математика Диофанта Александрийского.
Линейное ДУ представляется так:
a1x1+a2x2+a3x3+ …. + an-1xn-1+anxn=d
где d – некоторое целое число.
К понятию ДУ примыкает знаменитая «Великая теорема Ферма»[19], гласящая, что для любого натурального n>2, уравнение xn+yn=zn не имеет целых решений. Другими словами, подобное ДУ неразрешимо. Для n=2, решение лежит на поверхности: x=3, y=4, z=5.
Ироничный французский математик (на то, он и француз) Пьер Ферма в 1637 году на полях книги «Арифметика», все того же Диофанта, написал: «Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата, и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него».
Узость полей «Арифметика» Диофанта заставили лучших (и не только) математиков почти 360 лет искать доказательство теоремы Ферма. Только в 1995 году профессор Принстонского университета Эндрю Джон Уайлс публикует наиболее полное (на сегодня) корректное доказательство Великой теоремы Ферма.
Конечно, задание, которое будет стоять перед нашим генетическим алгоритмом, не идет ни в какое сравнение с проблемой Ферма и Уайлса.
ГА должен наметить путь поиска корней линейного ДУ с четырьмя переменными:
x+2y+3z+4t=30.
3.3. Начальная популяция (родители)
Предположив, что корни уравнения лежат на отрезке [1;30], выберем начальную популяцию из пяти особей (генотипов) – строк, включающих четыре случайных числа (гена) от 1 до 30, потенциальных корней решаемого ДУ:
Особь 1 – (1,28,15,3);
Особь 2 – (14,9,2,4);
Особь 3 – (13,5,7,3);
Особь 4 – (23,8,16,19);
Особь 5 – (9,13,5,2).
Подставим поочередно данный массив чисел в левую часть уравнения и сравним полученные значения с правой частью, числом 30. По сути, применим функцию приспособленности к каждому генотипу.
Результаты обработки сведем в Таблицу 1:
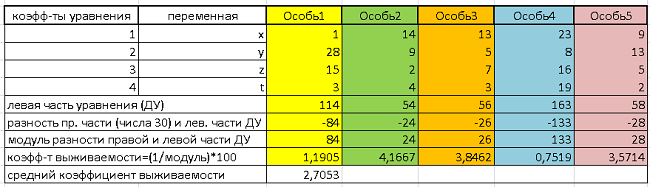
Таблица 1
Комментарии.
В первой и второй колонках обозначены коэффициенты и переменные ДУ. В следующих – заданные генотипы. Каждая особь отражена четырьмя числами (генами), обозначенными по тексту выше.
Далее, для каждой особи считается левая часть уравнения. Затем, для каждой особи берется модуль разности правой части ДУ (числа 30) и получившегося значения левой части. Таким образом, начинает работать функция приспособленности. Для формализации итоговых данных ФП, вычисляется величина, обратная найденному модулю, и умножается на 100. Полученный показатель назовем «коэффициентом выживания» (кратко, КВ). Чем он выше, тем исследуемый генотип имеет большее право идти дальше.
КВ лежит в диапазоне от 0,75 (Особь 4), худший результат, до 4,17 (Особь2) – «победитель соревнования». Среднее арифметическое значение КВ равно 2,71.
Переходим к размножению, через скрещивание, к кроссоверу.
Отберем случайным образом пять пар родителей (особей). Генератор случайных чисел настроим так, чтобы он учитывал коэффициенты выживания. Вероятность выпадения особи должна быть пропорциональна ее КВ. Вообразим многомерный куб со ста гранями. На 31-ой грани нанесен значок лучшей Особи2, на 28-ми гранях – значок Особи3, у которой результаты чуть похуже и т.д. Наименьшее количество граней заслужила Особь4 – 6. Число граней пропорционально весу КВ каждой особи.
Кидаем «сто-сторонний кубик» десять раз (пять раз по два). Пары для скрещивания вполне могут иметь следующий вид:
Особь3-Особь1;
Особь5-Особь2;
Особь3-Особь5;
Особь2-Особь5;
Особь5-Особь3.
Главный лузер, Особь4, вообще не выпала. Победитель (Особь2) появляется дважды. Остальные участники – крепкие середняки.
Для краткости, рассмотрим потомство одной, первой пары: Особь3-Особь1.
Кроссовер происходит путем разрывов строк (ДНК) каждой особи и соединения получившихся кусочков в ДНК ребенка.
Процесс скрещивания отображен в Таблице 2:
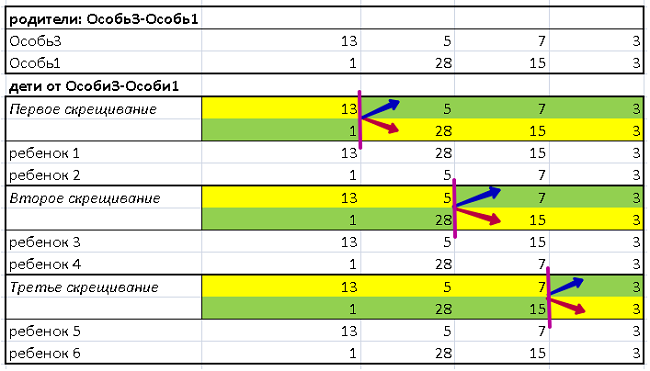
Таблица 2
В верхней части представлен генотип родителей. В нижней – детей после трех скрещиваний. Разрыв цепочки родительской ДНК проходит по границе смены цветов, с желтого на зеленый и с зеленого на желтый (вертикальный отрезок розового цвета)
При первом скрещивании, часть ДНК Особи3 с одним геном «13» (желтое поле) по красной стрелке сшивается с фрагментом ДНК Особи 1, строка (28,15,3) на желтом поле. Рождается ребенок1 (13, 28, 15, 3).
Здесь же, кусочек ДНК Особи1 с одним геном «1» (зеленое поле) по синей стрелке сшивается с фрагментом ДНК Особи 3, строка (5,7,3) на зеленом поле. Рождается ребенок2 (1, 5, 7, 3).
Алгоритм второго и третьего кросссовера работает также. Розовая граница разрыва строки перемещается вправо.
Итог – от пары родителей Особь3-Особь1 рождаются 6 детей: ребенок1, ребенок2…ребенок6.
Настало время проверить потомство от первой пары на функцию выживаемости и сравнить результат с достижениями «пап и мам».
Строим Таблицу 3, аналогичную Таблице 1:
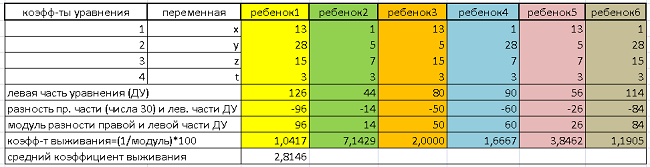
Таблица 3
Прогресс налицо.
Средний коэффициент выживания повысился до 2,81 (у родителей КВ=2,70). Лучшее дитя – Ребенок2 существенно превзошло лучшего родителя (Особь2). По КВ: 7,14 против 4,17. Что уж говорить о «родных папах и мамах» (Особей 3 и 1) с КВ 3,84 и 1,19 соответственно.
3.5. Продолжение процесса и остановка
Далее – стандартные этапы ГА.
Скрещиваются 4 оставшиеся пары. К детям применяется функция приспособленности. Отбираются лучшие индивидуумы, по определенной системе «разбавляются» не очень удачными ровесниками и вновь – скрещивание, селекция и формирование нового поколения. Вплоть до остановки алгоритма согласно условиям, описанными в общем виде выше.
Результат может считаться достигнутым, когда левая часть уравнения будет отличаться от правой (числа 30), допустим, не более, чем на 0,00001 или, предположим, когда КВ преодолеет отметку 10000. Все решает разработчик.
Так интересно соединяются биогенетика гороха и алгогенетика уравнения.
Владимир Наливайский
(источник – Википедия, если не оговорено иное)
- ↑ «Старобрненский монастырь»
- ↑ «Мендель, Грегор Иоганн»
- ↑ «Генетика»
- ↑ «Естественный отбор»
- ↑ «Геном»
- ↑ДНК – дезоксирибонуклеиновая кислота — одна из трех макромолекул (две другие – РНК и белки), обеспечивающая хранение, передачу из поколения в поколение и реализацию генетической программы развития и функционирования живых организмов
- ↑ РНК – одна из трех макромолекул (две другие – ДНК и белки), которые содержатся в клетках всех живых организмов и играют важную роль в кодировании, прочтении, регуляции и выражении генов
- ↑ «Дезоксирибонуклеиновая кислота»
- ↑ «Генотип»
- ↑ «Геном человека»
- ↑ «Репликация ДНК»
- ↑ «Рекомбинация (биология)»
- ↑ «Селекция»
- ↑ «Генетический алгоритм»
- ↑ «Холланд, Джон Генри»
- ↑ «Функция приспособленности»
- ↑ «Генетический алгоритм. Просто о сложном», Habr, 20.09.2011
- ↑ «Диофантово уравнение»
- ↑ «Великая теорема Ферма»
ДНК – дезоксирибонуклеиновая кислота
ГА – генетический алгоритм
ФП – функция приспособленности
ДУ – Диофантово уравнение
КВ – коэффициент выживания (для раздела 3 текста)
