Первая часть обзора методик, приемов, элементов инвестиционных стратегий компании Renaissance Technologies LLC Джеймса Саймонса. Хронология развития, участие и вклад отдельных персоналий. Связь с профильными разделами математики и статистики. Дополняет блогерский материал сайта о Renaissance.
Содержание:
- Введение. О скромности
- “Формула успеха” от Renaissance
- Количественные финансы и кванты
- “Лучший департамент физики и математики”
- Марковские и немарковские процессы
- Скрытая марковская модель и алгоритм Баума-Велша
Алгоритмы оптимизации (сходимости)
С чего начинается знакомство с компанией в век интернета?
С ее официального веб-ресурса. Пользователь вбивает в поисковую строку Google или Yandex название и кликает на поле “официальный сайт” или просто на самое верхнее сообщение, выдаваемое поисковой машиной. Что обычно совпадает. По крайней мере, для известных и крупных имен. Раскрывается электронный портал с более или менее современным дизайном и удобной навигацией.
Компании, позиционирующие себя, как лидеры отрасли, выбирают продвинутые варианты архитектуры корпоративного сайта, приглашают ведущих веб-мастеров. Например, еще совсем недавно в России на слуху была Студия Артемия Лебедева. По версии экспертной группы “Тэглайн”, она семь лет (до 2013 г.) возглавляла Топ-100 веб-студий Рунета. “Арт. Лебедев” автор сайтов Газпрома, российской версии Microsoft, Лента.ру, Билайн, Газета.ру и т.д.[1].
Солидно и престижно. Виртуальный посетитель имеет возможность оценить основательность предприятия, хозяина ресурса. Вписанная мелким шрифтом в самом низу главной страницы строчка “Сделано в Студии Артемия Лебедева” с узнаваемым логотипом[2] добавит презентабельности.
Если обратится к списку лидеров хедж-инвестирования, то образцом хорошего вкуса представляется портал компании Citadel LLC Кеннета Гриффина. Вряд ли Гриффину подставил плечо Артемий Лебедев. Скорей всего, сайт создан собственными силами. Кого-кого, а IT-специалистов в Цитадели хватает.
Посетитель ресурса может углубиться в историю компании, увидеть приятные, открытые, располагающие к доверию лица топ-менеджеров с перечнем их безусловных достижений в бизнесе, список офисов компании от Нью-Йорка до Гонконга. Здесь же принципы инвестирования и политика по рискам. Конечно, общие слова, а как иначе? Для визитки достаточно.
Фон выполнен в виде небоскребов Манхэттена с бегущими облаками и прочих, захватывающих дух, картинок мировых финансовых центров. Торговые залы с десятками мониторов, испещренных графиками и котировками. Энергичные (и надо полагать, компетентные) молодые мужчины и женщины в деловых костюмах. Понятные и одновременно завораживающие лозунги: “Сильные основы и Великие высоты”, “Мы победим честно”, “Заглянуть за горизонт рынка” и пр.
Все продумано, выверено и эффектно подано одним из лидеров мирового инвестиционного рынка с AUM (активами) $32,9 млрд по итогам второго квартала 2019 г.[3]. Девятое место в списке по данному показателю.
Это уровень.
Вторую строчку с AUM $68 млрд занимает Renaissance Technologies LLC (RT) геометра и тополога Дж. Саймонса. Выйти на официальный сайт RT путем введения ключа в поисковую строку Google трудновато. Проще - через профильные статьи в Википедии, индексируемые в верхнюю часть списка.
Впрочем, можно и не трудиться. Ничего особенно полезного по адресу rentec.com сторонний пользователь не извлечет. Он вообще мало, что извлечет. Домашняя страница с двумя адресами, в восточном Сетаукете и Нью-Йорке, список вакансий и вход для зарегистрированных инвесторов.
Все.
Bloomberg: “Даже сегодня веб-сайт компании выглядит так, словно он пришел из эры Netscape”[4].

“Формула успеха” от Renaissance
В контексте приведенной сверхлаконичности, вглядимся в кредо Renaissance. Оно выложено на базовой странице портала и занимает целое предложение: “Renaissance Technologies is a quantitative investment management company trading in global financial markets, dedicated to producing exceptional returns for its investors by strictly adhering to mathematical and statistical methods”.
Renaissance Technologies - компания, по управлению инвестициями, посредством количественных подходов, торгующая на глобальных финансовых рынках, стремящаяся обеспечить исключительную доходность для своих инвесторов, строго придерживаясь математических и статистических методов.
Девиз звучит, как математическое определение. Все важно, ничего лишнего и укладывается в следующую “формулу успеха” от RT:
Renaissance:
(количественные математико-статистические методики в инвестировании) + (трейдинг с использованием самого широкого инструментария) = (исключительная доходность).
Или, скажем так:
Rms+Rtr=Rpr
“Исключительная доходность” в трактовке - не пустые слова и даже не рекламный слоган.
Просто факт. Не более, но и не менее.
За период 1988-2018 гг. флагманский фонд Renaissance, Medallion показал легендарные в хедж-индустрии 66/39%. Медальон, в среднем, поднял 66% дохода в год до налогов и комиссий и 39% - после. В три кризисных года 2000, 2007 и 2008-ой - 98%, 85% и вновь 98% соответственно. Единственный “отрицательный” год 1989 - минус 4,1%.
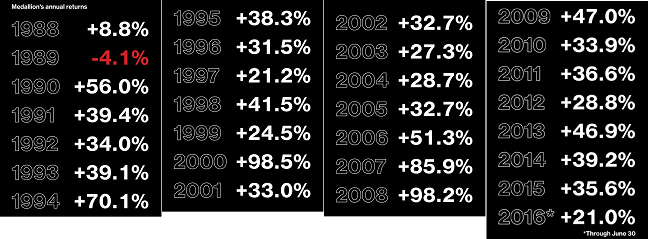
(источник[4])
Правая часть “формулы успеха” Renaissance, Rpr (profit) ясно выражена в числах: <Rpr>=66/39% в год за 1988-2018 гг.[5]
Стоит попытаться, пусть не разобраться (в рамках материала это невозможно, если это возможно вообще), но в общих чертах, в первом приближении, представить, что из себя представляют слагаемые формулы от Renaissance: Rms, математика и Rtr, финансовые инструменты и рынки.
Количественные финансы и кванты
“Суть математики в том, что никогда не знаешь, куда она приведет”
Джеймс Харрис Саймонс[28]
“Царица наук”[6] условно делится на две большие части: “чистую” и прикладную. Методы чистой математики помогают успешно решать разнообразные задачи в смежных научных дисциплинах (физике, химии, биологии), в технологиях, промышленности, транспорте (логистике), информатике, инженерном деле и бизнесе. Связь обоюдная. Попытки “математически” ответить на отдельные вопросы “из жизни” привели к зарождению и развитию целых разделов в математической теории.
Экономика и финансы не остались в стороне. Перефразируя Карла Маркса, серьезная наука не может не использовать математику[7]. А что серьезнее денег в этом мире? Среди прочих, появился предмет “Математические финансы” или “Финансовая математика”. Еще одно название - “Количественные финансы”, Quantitative Finance.
Главное предназначение матфинансов - математическое моделирование финансовых рынков.
У современных количественных финансов два направления[8]: исследование ценообразования деривативов и управление риском и инвестпортфелем. В первом - ключевую роль играет вероятность, не зависящая от риска (арбитражные операции), во втором - фактическая или актуарная вероятность.
Финансовый математик (инженер) существенно отличается от классического экономиста в подходах в изучении рыночных тенденций. По большому счету, количественного специалиста интересует всего одна вещь - куда пойдет (и насколько далеко) стоимость финансового актива: ценной бумаги (и/или ее производной) и товарного дериватива, включая валютные пары.
Его не слишком волнуют экономические фундаментальные причины ценообразования. Финансовый инженер попросту абстрагируется от них. Он создает одну за одной матмодель и вводит в нее массив известных (исторических) параметров: от стоимости анализируемой акции долю микросекунды назад до солнечной активности в период торговой сессии. Последнее - на уровне шутки, но, как известно, в каждой шутке…
Результат сравнивается с полученным через долю секунды или иной интервал времени фактическим значением переменной. Худшие модели отбрасываются, лучшие тестируются далее, с возможным изменением набора исходных данных. После ряда итераций нужно добиться минимального отклонения от реального рыночного итога. Предпочтение отдается “математической согласованности, а не совместимости с экономической теорией”.
Если матмодель успешно работает, количественный (квантовый) трейдер знает в какую сторону открывать позицию в инструменте (и открывать ли) и когда ее закрывать. Знает когда входить в рынок и когда выходить. Полученные навыки могут совершенно исключать сколько-нибудь глубокую осведомленность в макро- и микроэкономике. На практике, в разработке моделей неоценимую помощь оказывают астрофизики, социологи, лингвисты и метеорологи. Некоторые руководители крупных квантовых хедж-фондов приветствуют и весьма ценят такую экзотическую специализацию своих сотрудников.
Не случайно, в отношении подобных инвестиционных фирм часто применяют короткий термин “квантовый”, а не “количественный”. С латинского quantum означает “сколько”[9].
Чем не лозунг для финансиста-математика?
“Лучший департамент физики и математики”
Квантовые фонда не самые открытые структуры в мире. Их сотрудники не проводят семинары “Обучение трейдингу с нуля”, “Покупай, продавай, зарабатывай!” или “Узнай, как твои инвестиции могут работать за тебя!”.
Увы.
Специалисты успешных количественных хедж-фондов вообще не занимаются процессом внешнего обучения на основе опыта компании. Как правило, запрет на разглашение интеллектуальной собственности прописан в их контрактах. Нарушителям грозят судебное разбирательство и серьезные штрафы.
Renaissance Technologies LLC Дж. Самонса режим секретности поддерживать проще, чем иным “коллегам по цеху”, ввиду крайне низкой текучести персонала.
Содружество ученых сильно корпоративным духом и обладает хорошим кадровым иммунитетом по отношению к конкурентам на Уолл-стрит. Видный американский математик, автор индексной теоремы Атьи-Зингера[10], Айсадор Зингер, Isadore M. Singer окрестил офис Renaissance в восточном Сетаукете лучшим департаментом физики и математики в мире[11].
Марковские и немарковские процессы
Какие модели, методики и подходы использует RT для достижений своих заоблачных доходностей - тайна.
Саймонс с сотрудниками посмеиваются над домыслами о том, что делает Renaissance. Цитированный ранее профессор Массачусетского технологического института Эндрю Ло пишет: “Все мы в квантовом бизнесе строим догадки и гипотезы, однако имеем очень мало данных <о RT>. Вот почему мы любим рассуждать о том, чем именно может заниматься Renaissance. Они так далеко обошли всех остальных...”
В большей степени, это касается современного состояния дел в Renaissance Technologies LLC. Кое-что из прошлого компании и ее флагмана Medallion Fund стало достоянием “квантовой публики” и заставило удивиться и восхититься.
И породило большое число подражателей.
Когда речь заходит о раннем рывке Медальона и об его предшественниках - Monemetrics и Axcom Ltd (период 1982-1993 гг.) вспоминают о скрытых марковских моделях и алгоритме Баума-Велша.
По порядку.
О “марковости” в теории вероятности и матстатистике.
С точки зрения наличия/отсутствия “памяти” случайные (стохастические) процессы делятся на два класса: марковские и немарковские.
Доступно о марковских и немарковских процессах, названных в честь российского математика Андрея Маркова (1856-1922), изложено в материале о случайном блуждании в математике и физике.
Немарковский процесс - “случайный процесс, эволюция которого после любого заданного значения времени зависит от эволюции, предшествовавшей этому моменту времени”[12]. Проще говоря, немарковский процесс - эволюционное развитие с памятью.
Примеры немарковских процессов - фликкер-шум[13], некоторые радиотехнические сигналы, а также броуновское движение на малых временных интервалах. Интересно (почему - см. ниже), что к немарковским процессам могут отнести и такой случайный феномен в сложной среде, как изменение курса ценной бумаги.
Марковский процесс - «случайный процесс, эволюция которого после любого заданного значения времени не зависит от эволюции, предшествовавшей этому моменту времени, при условии, что значение процесса в этот момент фиксировано; «будущее» процесса не зависит от «прошлого» при известном «настоящем»[14]. Марковский процесс памяти не имеет.
На языке теории вероятностей, марковский процесс - случайный процесс с марковским свойством. Полагают, что процесс обладает марковским свойством, если “условное распределение вероятностей[15] будущих состояний процесса зависит только от нынешнего состояния, а не от последовательности событий, которые предшествовали этому”[16].
Марковский процесс представляется моделью авторегрессии первого порядка AR(1)[14]:
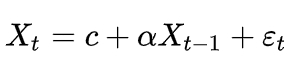
(формула 1)
где: Xt-1 и Xt - значение временного ряда в моменты времени t-1 и t;
α - параметр модели (коэффициент авторегрессии);
c - константа;
εt - шум.
Формула 1 описывает знаменитое случайное блуждание, которое, согласно гипотезе эффективного рынка (EMH), формирует цену финансового актива (акции и пр.) на бирже.
Парадоксальная интерпретация колебания цены на акцию одновременно. как марковский и немарковский процесс, представляет глубинный дуализм рассматриваемого явления. Своеобразный итог (компромисс) противостояния сторонников и противников EMH. Каждый оперирует и настаивает на своих аргументах. Ключевой довод - кто точнее предскажет рыночную ситуацию и больше заработает.
Renaissance сделал ставку на марковскую модель.
Скрытая марковская модель и алгоритм Баума-Велша
Математики Renaissance Technologies предположили, что движение котировки акции укладывается в “скрытую марковскую модель” и оптимизировали последнюю с помощью специальных алгоритмов сходимости.
СММ вводится на конечном множестве случайных переменных:
{y(0), y(1), y(2), ...y(n-1); x(0), x(1), x(2), ...x(n-1)}
где y(...) - известные (наблюдаемые) переменные, а x(...) - неизвестные (скрытые) значения. У каждого вектора (последовательности) X и Y длина (число членов) равна n. В общем случае, она может быть различной.
Скрытая марковская модель характеризуется двумя независимыми утверждениями, позволяющие проводить ее оптимизацию[18]:
1. P{(x(t)|[x(t-1), x(t-2), …x(0); y(t), y(t-1), y(t-2), ...y(0)]}=P[x(t)|x(t-1)].
На скрытое событие x(t) (значение события), влияет только скрытое событие, непосредственно ему предшествующее, x(t-1).
2. P{(y(t)|[x(t), x(t-1), x(t-2), …x(0); y(t-1), y(t-2), ...y(0)]}=P[y(t)|x(t)].
На наблюдаемое событие y(t) влияет только скрытое событие x(t), происходящее в данный момент времени t.
Условные вероятности P[x(t)|x(t-1)] и P[y(t)|x(t)] трактуют, как вероятности переходов между соответствующими состояниями.
Сказанное хорошо иллюстрируется следующим рисунком[17]:
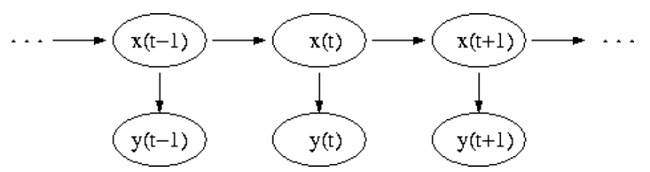
“Сетевой график” наглядно демонстрирует направление вышеописанных связей: x(t+1) зависит только от x(t), x(t) зависит от x(t-1) и т.д. В свою очередь, y(t+1) зависит только от x(t+1), y(t) только от x(t), y(t-1) от x(t-1) и т.д.
Вектор X скрытых значений называют иногда первым этапом СММ, вектор Y наблюдаемых значений - вторым этапом. В целом, такую наиболее простую архитектуру именуют “СММ первого порядка” или “обычной СММ”.
Вероятность появления цепочки Y={y(0), y(1), …. y(n-1)} длины n равна:
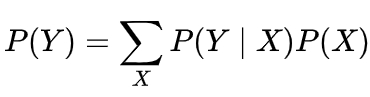
(формула 2)
Здесь сумма пробегает по всем значениям последовательности X={x(0), x(1), …. x(n-1)}.
Суть оптимизации СММ - нахождение экстремальных значений (максимумов) P(Y), другими словами, поиск векторов Y, отвечающих наибольшим P(Y).
Для более ясного понимания сущности СММ Википедия[17] предлагает забавную зарисовку с двумя друзьями. Назовем их Джоном и Джеком.
Гипотетический Джон умеет делать всего три вещи - гулять в парке, ходить за покупками и убираться в доме. Не очень, скажем яркая жизнь, но математики обожают подобные допущения в мысленных экспериментах. Выбор Джона определяется только погодой. Похоже Джон - англичанин, они помешаны на метеоусловиях. Математическая погода в городе Джона имеет только два состояния - солнечное или дождливое (точно Англия).
Джек живет далеко от Джона и общается с ним только по телефону. Джон, как настоящий британец, обожает порассуждать о погоде, но несколько странно.
Через загадки.
Он рассказывает Джеку только то, чем он занимается (парк, магазин, уборка) и предоставляет приятелю угадать, светит у него солнце или идет дождь.
Имеем типичную скрытую марковскую модель. Известные из телефонных бесед занятия Джона: прогулка в парке - y(парк), визит в магазин - y(магазин) и домашние хлопоты - y(уборка). Скрытые состояния капризной погоды: солнце - x(солнце) и дождь - x(дождь). Джек знает, чем занимается друг, но не ведает о погоде в его городе.
Видимые события “y” в виде времяпровождений Джона являются следствием
скрытых погодных условий “x”. Очевидно, что он не пойдет в парк, но вполне может затеять уборку, когда за окном стучит дождь. Напротив, солнечный день - логичная причина побегать по парковым дорожкам с собакой и покормить уток в пруду. Но - не обязательно. С другой стороны, после дождя должно выглянуть солнце. Опять же - не факт, особенно в изменчивом туманном Альбионе.
Если Джон и Джек висят на телефоне ежедневно на протяжении, скажем так, лет двух-трех (очень теоретические мужчины), то набрав хорошую статистику Джек обретет редкое качество - установить с хорошей степенью вероятности светит солнце или идет дождь в городе Джона, исходя из того, чем он занимается.
Зачем это нужно Джеку - большой вопрос. Для создателей мысленных экспериментов это не предмет для обсуждения. Может быть Джеку банально скучно. А возможно - он математик, тогда тяга к “играм разума” становится более понятной.
Но в других областях человеческой деятельности такие способности оказываются чрезвычайно важными. В распознавании речи (машинном переводе), в идентификации образов, движений, в анализе ДНК, в криптологии и т.д. и т.п.
И в математических финансах.
Посмотрим на скрытую марковскую модель с точки зрения фондового рынка. Предположим следующую конструкцию.
Трейдера интересует поведение тренда акции А в ближайшем будущем. Пойдет он вверх, вниз или будет двигаться горизонтально, вдоль некоторой средней линии.
Сформируем вектор X из трех скрытых значений: {x(↑), x(↓) и x(→)}.
Первое - x(↑), означает наличие существенных предпосылок (значительной вероятности) роста курса в некий промежуток времени (t; t+Δt). Второе, x(↓) - предпосылки снижения акции. Наконец, x(→) - боковой дрейф.
Не будем оригинальны и повторим опыт Джона-Джека. Только поменяем местами видимое и невидимое.
Вообразим, что последовательность наблюдаемых событий Y содержит значение y(солнце) - солнечная погода в Нью-Йорке и y(дождь) - в городе Большого Яблока, в районе Уолл-стрит, сыро. Если вы думаете, что приведенный набор полный бред, то в отношении Renaissance Technologies вы ошибаетесь. О подобных сигналах на конференции в 2013 году сообщал один из руководителей компании Питер Браун, бывший специалист по компьютерной лингвистике из IBM.
Прогнав многократно (много-соттысячнократно) обе ветки в СММ “Курс акции А - погода В Нью-Йорке” можно попытаться нащупать устойчивые связи с приемлемыми уровнями распределения вероятностей. Правды ради, надо отметить, что по словам П. Брауна, упомянутые метеорологические сигналы не оказались особенно полезными. Они попадали в цель лишь чуть более, чем в 50% случаев.
Но это ничего не значит. Сигналы надо искать.
Тот же П. Браун говорит: “Штука в том, что если вы находите сигнал, который был сильным и имел смысл, то его уже давно использовали в трейдинге… Что мы делаем, так это ищем множество сигналов. У нас сидят что-то около 90 докторов наук в области физики и математики, которые просто ищут такие сигналы весь день. У нас постоянно работают 10 000 процессоров, которые перерабатывают данные в поисках сигналов».
Искать максимумы P(Y) из формулы 2, переворачивая колоссальные массивы узлов и связей, по той или иной СММ, задача не просто трудоемкая. Работа “руками” - большая глупость с точки зрения прикладного математика. Он придумает алгоритмы и пропустит их через вычислительные мощности, способные обрабатывать big data, измеряемые терабайтами и петабайтами[19].
Будни Renaissance Technologies уже не один десяток лет.
Алгоритмы оптимизации (сходимости)
Для оптимизации скрытой марковской модели применяют три алгоритма[17]. Ограничимся их формальным описанием.
1. Алгоритм прямого-обратного хода[20].
Цепочка событий прогоняется в прямом направлении, от первого значения до последнего, с расчетом вероятностей прямых переходов. Далее проводится обратное движение с вычислением вероятностей обратных переходов. Перемещения по веткам СММ в противоположных направлениях повторяется многократно. При каждом прогоне проводится сглаживание распределения полученных вероятностей прямых-обратных переходов.
2. Алгоритм Витерби[21].
Предложен американским инженером Эндрю Джеймсом Витерби, Andrew James Viterbi, в 1967 году. Во многом благодаря алгоритму Витерби появились мобильная телефония стандартов GSM и CDMA, dial-up модемы и многое другое.
Алгоритм (путь Витерби) ищет наиболее вероятную последовательность скрытых узлов, достоверно отражающую видимые элементы СММ.
3. Алгоритм Баума-Велша.
Максимизирует вероятность P(Y) из формулы 2 путем подбора параметра λ по заданному вектору Y[y(0), y(1), … y(n-1)]:
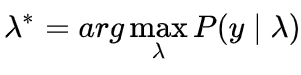
(формула 3) [18]
λ определяется, как λ=(A, B, π).
Здесь A - матрица вероятностей переходов (стохастическая матрица перемещений) по узлам X, B - матрица вероятностей переходов между узлами Y и X. π - совсем не число π (3,14….), а начальное состояние (распределение вероятностей) в последовательности X.
Все довольно сложно, но, к сожалению углубиться в суть вопроса в предлагаемом материале нет никакой возможности. Для расширения кругозора следует обратиться к приведенным в примечаниях статьям из Википедии, и в них походить по ссылкам.
"Знак четырех": Саймонс, Баум, Акс и Берлекамп
История успеха звезды Renaissance Technologies - фонда Медальон тесно связана с именами трех математиков, привлеченных Джеймсом Саймонсом к сотрудничеству.
Леонард Исау Баум, Leonard Esau Baum (1931-2017), Джеймс Бартон Акс, James Burton Ax (1937-2006) и Элвин Ральф Берлекамп, Elwyn Ralph Berlekamp (1940-2019). Все ровесники Саймонса (1938 года рождения) и все уже ушли в лучший мир.
Буквально, несколько слов о каждом. Почувствуйте, какими неординарными личностями окружал себя Джеймс Самонс. В то время такие редко забредали на Уолл-стрит.
Леонард Баум.
Один из авторов алгоритма Баума-Велша, разработанного им вместе с Ллойдом Р. Велшем в Институте оборонного анализа США, Institute for Defense Analyses (IDA). В IDA четыре года (1964-68) криптологом трудился Саймонс, там они и познакомились. Научные пристрастия Баума были сосредоточены на банаховой алгебре[22], криптологии, генетике и распознавании речи. После ухода из Медальона работал в области теории простых чисел и гипотезы Римана. Досуг посвящал игре в Го, принимая неоднократное участие в серьезных турнирах[23].
Джеймс Акс.
Достиг значительных результатов в современной алгебре и теории чисел, применяя раздел математической логики - теорию моделей[24]. Интересовался проблемами фундаментальной физики, в частности аксиоматизацией пространственно-временного континуума и квантовой механики. Вклад в теорию чисел Дж. Акса отмечен премией Френка Нельсона Коула[25].
В конце жизненного пути, кроме точных наук, Акс изучал основы драматургии и сценарного дела. В 2005 году успел закончить сценарий триллера “Боты” (Bots).
Специалист в теории кодирования и комбинаторной теории игр. Соавтор алгоритмов Берлекампа-Велша и Берлекампа-Масси, используемых в кодах коррекции ошибок Рида-Соломона[26]. Известный эксперт по матметодам в играх. Принимал участие в подготовке книг “Математическое Го”, “Пути побед в ваших математических играх”[27].

Э. Берлекамп в 2005 г.[27]
Исходя из доступных сведений, драма с участием четырех математиков в пьесе “Medallion Fund” разворачивалась следующим образом.
В 1978 г. Дж. Саймонс покидает матфак университета в Стоуни-Брук и пытается сосредоточиться на трейдинге. Учреждается компания Monemetrics. Вначале Саймонсу не очень везет. Ему как-то не приходит в голову сделать ставку на математику и математиков. Как только он поменял тактику, успех не заставил себя долго ждать. “Сначала я нанял экономистов, но дело не пошло. И тогда я пригласил математиков, потому что понял: нужно иметь дело с тем, в чем разбираешься”[28].
Первым пришел Баум, коллега Саймонса по институту оборонного анализа десять лет назад. До и после Monemetrics Баум не слыл особым активистом матмоделей в инвестировании и ориентировался на фундаментальную торговлю. Но в конце 1970-х - начале 1980-х он оказал фонду Саймонса неоценимую услугу, рассматривая финансовые рынки, как скрытые марковские модели и последовательно применяя алгоритм своего имени для их оптимизации. Дж. Саймонс вспоминал: “После того, как я вовлек Лени, я смог увидеть возможности построения моделей”.
Главным объектом для Баума стал рынок forex. Спустя некоторое время в связке Саймонс-Баум что-то пошло не так. Некоторые источники ссылаются на пиковые просадки на методиках Лео[23]. Саймонсу ситуация не понравилась, и в 1984 г. Баум покидает фирму.
Баума сменяет Джеймс Акс. Он совершенно предсказуемо расширяет область разработок своего предшественника на фондовый и срочный рынки, включая деривативы с товарным базовым активом. Дела пошли в гору. Саймонс и Акс открывают Axcom Ltd[29], непосредственного предшественника Medallion Fund.
Сын Джеймса Акса писал о талантах отца: “Он отличался способностью видеть структуры в торговой информации, Люди считали это волшебством или вздором”. Кроме гениальности, Акс отличался непростым характером что присуще одаренным людям. С ними нелегко и членам семьи, и коллегам. В работе Акс проявлял сильнейшее упрямство. Сбить с намеченного курса будущего сценариста было нереально.
Когда в апреле, единственного несчастливого для Медальона 1989 года, убытки вышли на уровень 30%, Акс оправдал свою фамилию на 100%[30]. Саймонс потребовал закрыть позиции и дополнительно протестировать модели. Акс ответил в том духе, что все нормально, беспокоиться не о чем, такой отрицательный результат учтен в его алгоритмах и надо продолжать. Терпение Саймонса лопнуло, Акс пригрозил судом и хлопнул дверью.
Ушел заниматься квантами, но уже в физике, а не в трейдинге, и учиться “на Шекспира”. Талантливому человеку всегда есть, чем заняться. На торговле акциями свет клином не сошелся.
На сцене появляется Элвин Берлекамп.
Энергичный профессор математики из Беркли, с доверчивым взглядом серых глаз, проявил жесткую хватку бизнесмена. Свою карьеру в Renaissance он начал с покупки доли Дж. Акса в Axcom и перезапуска его программ.
В 1990-м году Медальон выходит на 59% годового дохода. В последующие 25 лет ставка доходности вложений акционеров фонда не опускаются ниже 21% в год (до налогов).
Берлекамп резюмировал: “Я был уверен, что модели будут работать лучше. Я не думал, что они будут настолько хороши”.
Через 16 месяцев после покупки акций Axcom, он продает свой пакет Саймонсу с наценкой в 500% и возвращается к преподаванию математики в Калифорнийском университете. “Я получал намного больше удовольствия от общения с учеными, чем c финансовыми типами, - говорит Берлекамп. – Большинство людей в этом бизнесе довольно-таки доллароцентричны. Это делает жизнь скучной».
Так создавалась историческая цепь: Monemetrics-Axcom-Medallion.
Продолжение темы Renaissance Technologies смотрите в следующей части материала.
При подготовке текста использовалась информация статьи K. Burton “ Inside a Moneymaking Machine Like No Other”, Bloomberg, 21.11.2016, в редакции перевода портала Ain.ua, а также материалы ресурса MMGP.
Примечания и ссылки (источник – Википедия/Wikipedia или авторский комментарий, если не оговорено иное).
- “Студия Артемия Лебедева”.
- Официальный сайт ПАО “Газпром”.
- “List of hedge funds”.
- K. Burton “ Inside a Moneymaking Machine Like No Other”, Bloomberg, 21.11.2016, в редакции перевода портала Ain.ua
- <X> - среднее значение величины X.
- “Математика - Царица наук”, - Карл Ф. Гаусс.
- Цитата от Карла Маркса: “Наука только тогда достигает совершенства, когда она начинает пользоваться математикой”.
- “Mathematical finance”.
- “Квант”.
- “Atiyah–Singer index theorem”.
- “Renaissance Technologies”, англ.
- “Немарковский процесс”.
- Фликкер-шум, фликкерный шум, 1/f шум - электронный шум, наблюдаемый практически в любых аналоговых электронных устройствах; его источниками могут являться неоднородности в проводящей среде, генерация и рекомбинация носителей заряда в транзисторах и т. п., “Фликкер-шум”.
- “Марковский процесс”.
- Условная вероятность — вероятность наступления события А при условии, что событие B произошло: P(A|B), “Условная вероятность”.
- “Марковское свойство”.
- “Скрытая марковская модель”.
- “Алгоритм Баума-Велша”.
- 1 Терабайт (Тбайт) = 1012 Байт, 1 Петабайт (Пбайт) = 103 Тбайт.
- “Алгоритм прямого обратного хода”
- “Алгоритм Витерби”
- “Банахова алгебра”.
- “Leonard E. Baum”.
- “Теория моделей”.
- “James Ax”.
- “Reed–Solomon error correction”.
- “Elwyn Berlekamp”.
- К Гилева “Трейдер-математик. Джим Саймонс”, “Открытый журнал” (компания “Открытие Брокер”), 22.03.2019.
- Согласно [25] - Axcom Trading Advisors.
- “Axe” по-английски - топор.
RT - Renaissance Technologies LLC, коротко, Renaissance
AUM - Assets Under Management, активы под управлением
EMH – Efficient Market Hypothesis, гипотеза эффективного рынка
СММ - скрытая марковская модель
IDA - Institute for Defense Analyses, Институт оборонного анализа США
